Question

【题目】如图所示为火车站装载货物的原理示意图，设AB段为斜面，水平段BC使用水平传送带装置，BC长L=8m，与货物包的动摩因数μ=0.6，皮带轮的半径为R=0.2m，上部距车厢底面的高度h=0.45m．货物从A点下滑，进入BC段时初速度v0 =10m/s．通过调整皮带轮（不打滑）的转动角速度ω可使货物经C点抛出后落在车厢上的不同位置，取g=10m/s2，求：

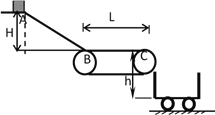
（1）当皮带轮静止时，货物包在车厢内的落地点到C点的水平距离；

（2）当皮带轮以角速度ω=20 rad/s顺时方针方向匀速转动时，包在车厢内的落地点到C点的水平距离；

（3）若皮带轮顺时方针方向转动，试写出货物包在车厢内的落地点到C点的水平距离s随皮带轮角速度 变化关系．（只写结果，不写过程）

Answer 1

【答案】（1） （2） （3）

Ⅰ、0≤ω≤10 rad/s时， S=0.6m

II、10＜ω＜50 rad/s时， S= 0.06ω

III、50＜ω＜70 rad/s时， S= 0.06ω

Ⅳ、ω≥70 rad/s时， S=4.2m

【解析】货物从B到C做匀减速运动，加速度a==μg=6m/s2；
设到达C点速度为VC，则：v02-vC2=2aL，解得：VC=2m/s，
在C处，由牛顿第二定律得：m＝10m＝mg，
可知此时重力恰好充当向心力，货物在C处立刻做平抛运动．
落地点到C点的水平距离：s=vCt=vC =0.6m；
（2）皮带速度V皮=ωR=4m/s，由（1）的论证可知：v皮＞vC，
货物先减速后匀速，从C点抛出的速度为vC′=4m/s，
落地点到C点的水平距离：s′=vC′t=vC′=1.2m；
（3）Ⅰ、0≤ω≤10rad/s时，S=0.6m，
II、10＜ω＜50rad/s时，S=ωR=0.06ω
III、50＜ω＜70rad/s时，S=ωR=0.06ω
Ⅳ、ω≥70rad/s时，S=vC=4.2m；