题目内容
3.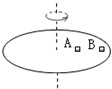 如图所示,两个质量均为m的小木块A和B(可视为质点)放在水平圆盘上,A与转轴的距离为L,B与转轴的距离为2L.木块与圆盘的最大静摩擦力为木块所受重力的k倍,重力加速度大小为g.若圆盘从静止开始绕转轴缓慢地加速转动,用ω表示圆盘转动的角速度,下列说法正确的是( )
如图所示,两个质量均为m的小木块A和B(可视为质点)放在水平圆盘上,A与转轴的距离为L,B与转轴的距离为2L.木块与圆盘的最大静摩擦力为木块所受重力的k倍,重力加速度大小为g.若圆盘从静止开始绕转轴缓慢地加速转动,用ω表示圆盘转动的角速度,下列说法正确的是( )| A. | B一定比A先滑动 | |
| B. | A、B所受静摩擦力始终相等 | |
| C. | ω=$\sqrt{\frac{kg}{2L}}$是B开始滑动的临界角速度 | |
| D. | 当ω=$\sqrt{\frac{2kg}{3L}}$时,A所受的摩擦力大小为kmg |
分析 木块随圆盘一起转动,静摩擦力提供向心力,而所需要的向心力大小由物体的质量、半径和角速度决定.当圆盘转速增大时,提供的静摩擦力随之而增大.当需要的向心力大于最大静摩擦力时,物体开始滑动.因此是否滑动与质量无关,是由半径大小决定.
解答 解:A、B、两个木块的最大静摩擦力相等.木块随圆盘一起转动,静摩擦力提供向心力,由牛顿第二定律得:木块所受的静摩擦力f=mω2r,m、ω相等,f∝r,所以b所受的静摩擦力大于a的静摩擦力,当圆盘的角速度增大时b的静摩擦力先达到最大值,所以b一定比a先开始滑动,故A正确,B错误;
C、当b刚要滑动时,有kmg=mω2•2l,解得:ω=$\sqrt{\frac{kg}{2L}}$,故C正确;
D、以a为研究对象,当ω=$\sqrt{\frac{2kg}{3L}}$时,由牛顿第二定律得:
f=mω2L,可解得:f=$\frac{2}{3}$kmg,故D错误.
故选:AC
点评 本题的关键是正确分析木块的受力,明确木块做圆周运动时,静摩擦力提供向心力,把握住临界条件:静摩擦力达到最大,由牛顿第二定律分析解答.

练习册系列答案
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
10.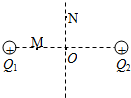 如图所示,Q1、Q2为二个等量同种的正点电荷,在二者的电场中有M、N和O三点,其中M和O在Q1、Q2的连线上(O为连线的中点),N为过O点的垂线上的一点.则下列说法中错误的是( )
如图所示,Q1、Q2为二个等量同种的正点电荷,在二者的电场中有M、N和O三点,其中M和O在Q1、Q2的连线上(O为连线的中点),N为过O点的垂线上的一点.则下列说法中错误的是( )
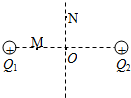 如图所示,Q1、Q2为二个等量同种的正点电荷,在二者的电场中有M、N和O三点,其中M和O在Q1、Q2的连线上(O为连线的中点),N为过O点的垂线上的一点.则下列说法中错误的是( )
如图所示,Q1、Q2为二个等量同种的正点电荷,在二者的电场中有M、N和O三点,其中M和O在Q1、Q2的连线上(O为连线的中点),N为过O点的垂线上的一点.则下列说法中错误的是( )| A. | 在Q1、Q2连线的中垂线位置可以画出一条电场线 | |
| B. | 若将一个正点电荷分别放在M、N和O三点,则该点电荷在M点时的电势能最大 | |
| C. | 若ON间的电势差为U,ON间的距离为d,则N点的场强为$\frac{U}{d}$ | |
| D. | 若ON间的电势差为U,将一个带电量为q的负点电荷从N点移到O点,则克服电场力做功为Uq |
11.如图所示,一个带正电的粒子以垂直于磁感线的方向进入匀强磁场中时,它所受洛仑兹力的方向是( )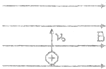

| A. | 水平向左 | B. | 水平向右 | C. | 垂直于纸面向里 | D. | 垂直于纸面向外 |
8. 如图所示,大小可以不计的带有同种电荷的小球A和B互相排斥,静止时两球位于同一水平面上,绝缘细线与竖直方向的夹角分别为α和β,且α<β,由此可知( )
如图所示,大小可以不计的带有同种电荷的小球A和B互相排斥,静止时两球位于同一水平面上,绝缘细线与竖直方向的夹角分别为α和β,且α<β,由此可知( )
 如图所示,大小可以不计的带有同种电荷的小球A和B互相排斥,静止时两球位于同一水平面上,绝缘细线与竖直方向的夹角分别为α和β,且α<β,由此可知( )
如图所示,大小可以不计的带有同种电荷的小球A和B互相排斥,静止时两球位于同一水平面上,绝缘细线与竖直方向的夹角分别为α和β,且α<β,由此可知( )| A. | B球带的电荷量较多 | |
| B. | B球质量较大 | |
| C. | B球受的拉力较大 | |
| D. | 两球接触后,再静止下来,两绝缘细线与竖直方向的夹角变为α′、β′,则仍有α′<β′ |
15. 如图所示,质量为m1的木块和质量为m2的长木板叠放在水平地面上.现对木块施加一水平向右的拉力F,木块在长木板上滑行,而长木板保持静止状态.己知木块与长木板间的动摩擦因数为μ1,长木板与地面间的动摩擦因数为μ2,且最大静摩擦力与滑动摩擦力相等.下列说法正确的是( )
如图所示,质量为m1的木块和质量为m2的长木板叠放在水平地面上.现对木块施加一水平向右的拉力F,木块在长木板上滑行,而长木板保持静止状态.己知木块与长木板间的动摩擦因数为μ1,长木板与地面间的动摩擦因数为μ2,且最大静摩擦力与滑动摩擦力相等.下列说法正确的是( )
 如图所示,质量为m1的木块和质量为m2的长木板叠放在水平地面上.现对木块施加一水平向右的拉力F,木块在长木板上滑行,而长木板保持静止状态.己知木块与长木板间的动摩擦因数为μ1,长木板与地面间的动摩擦因数为μ2,且最大静摩擦力与滑动摩擦力相等.下列说法正确的是( )
如图所示,质量为m1的木块和质量为m2的长木板叠放在水平地面上.现对木块施加一水平向右的拉力F,木块在长木板上滑行,而长木板保持静止状态.己知木块与长木板间的动摩擦因数为μ1,长木板与地面间的动摩擦因数为μ2,且最大静摩擦力与滑动摩擦力相等.下列说法正确的是( )| A. | 木块受到的摩擦力大小为μ1(m1+m2)g | |
| B. | 长木板受到的摩擦力大小为μ2(m1+m2)g | |
| C. | 若改变F的大小,当F>μ1(m1+m2)g时,长木板一定不运动 | |
| D. | 若将F作用于长木板,长木板与木块有可能会相对滑动 |
13.已知一宇宙飞船绕地球做匀速圆周运动的周期为T,距离地面高度为h,地球半径为R,引力常量为G,则地球的质量为( )
| A. | $\frac{4{π}^{2}(R+h)^{3}}{G{T}^{2}}$ | B. | $\frac{4{π}^{2}(R+h)^{2}}{G{T}^{2}}$ | C. | $\frac{2{π}^{2}(R+h)}{G{T}^{2}}$ | D. | $\frac{2{π}^{2}(R+h)^{3}}{G{T}^{2}}$ |

 一透明半圆柱的横截面如图所示,圆心为O,一束光线在横截面内从C点沿垂直于直径AB的方向入射,在半圆柱内沿图示路径传播,最后从E点射出半圆柱.已知圆半径为R=0.30m,半圆柱折射率为n=2.0,∠AOC=30°,真空中的光速为c=3.0×108m/s.求光线在半圆柱内沿图示C→D→E路径传播的时间(结果保留两位有效数字).
一透明半圆柱的横截面如图所示,圆心为O,一束光线在横截面内从C点沿垂直于直径AB的方向入射,在半圆柱内沿图示路径传播,最后从E点射出半圆柱.已知圆半径为R=0.30m,半圆柱折射率为n=2.0,∠AOC=30°,真空中的光速为c=3.0×108m/s.求光线在半圆柱内沿图示C→D→E路径传播的时间(结果保留两位有效数字).