题目内容
13.已知一宇宙飞船绕地球做匀速圆周运动的周期为T,距离地面高度为h,地球半径为R,引力常量为G,则地球的质量为( )| A. | $\frac{4{π}^{2}(R+h)^{3}}{G{T}^{2}}$ | B. | $\frac{4{π}^{2}(R+h)^{2}}{G{T}^{2}}$ | C. | $\frac{2{π}^{2}(R+h)}{G{T}^{2}}$ | D. | $\frac{2{π}^{2}(R+h)^{3}}{G{T}^{2}}$ |
分析 根据万有引力定律公式求出地球对卫星的万有引力大小.结合万有引力提供向心力求解.
解答 解:卫星作匀速圆周运动,根据万有引力充当向心力得:
$G\frac{Mm}{(R+h)_{\;}^{2}}=m\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}(R+h)$
解得:$M=\frac{4{π}_{\;}^{2}(R+h)_{\;}^{3}}{G{T}_{\;}^{2}}$,故A正确,BCD错误
故选:A
点评 万有引力定律常用方程有(1)星球表面的重力和万有引力相等;(2)环绕天体受到的万有引力提供向心力.这是解决这类问题常用的方程,要注意环绕天体运动半径的表述.

练习册系列答案
相关题目
3.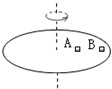 如图所示,两个质量均为m的小木块A和B(可视为质点)放在水平圆盘上,A与转轴的距离为L,B与转轴的距离为2L.木块与圆盘的最大静摩擦力为木块所受重力的k倍,重力加速度大小为g.若圆盘从静止开始绕转轴缓慢地加速转动,用ω表示圆盘转动的角速度,下列说法正确的是( )
如图所示,两个质量均为m的小木块A和B(可视为质点)放在水平圆盘上,A与转轴的距离为L,B与转轴的距离为2L.木块与圆盘的最大静摩擦力为木块所受重力的k倍,重力加速度大小为g.若圆盘从静止开始绕转轴缓慢地加速转动,用ω表示圆盘转动的角速度,下列说法正确的是( )
 如图所示,两个质量均为m的小木块A和B(可视为质点)放在水平圆盘上,A与转轴的距离为L,B与转轴的距离为2L.木块与圆盘的最大静摩擦力为木块所受重力的k倍,重力加速度大小为g.若圆盘从静止开始绕转轴缓慢地加速转动,用ω表示圆盘转动的角速度,下列说法正确的是( )
如图所示,两个质量均为m的小木块A和B(可视为质点)放在水平圆盘上,A与转轴的距离为L,B与转轴的距离为2L.木块与圆盘的最大静摩擦力为木块所受重力的k倍,重力加速度大小为g.若圆盘从静止开始绕转轴缓慢地加速转动,用ω表示圆盘转动的角速度,下列说法正确的是( )| A. | B一定比A先滑动 | |
| B. | A、B所受静摩擦力始终相等 | |
| C. | ω=$\sqrt{\frac{kg}{2L}}$是B开始滑动的临界角速度 | |
| D. | 当ω=$\sqrt{\frac{2kg}{3L}}$时,A所受的摩擦力大小为kmg |
18. 如图所示,桌面高度为h,质量为m的小球,从离桌面高H处自由落下,不计空气阻力,假设桌面处的重力势能为零,关于重力势能的说法正确的是( )
如图所示,桌面高度为h,质量为m的小球,从离桌面高H处自由落下,不计空气阻力,假设桌面处的重力势能为零,关于重力势能的说法正确的是( )
 如图所示,桌面高度为h,质量为m的小球,从离桌面高H处自由落下,不计空气阻力,假设桌面处的重力势能为零,关于重力势能的说法正确的是( )
如图所示,桌面高度为h,质量为m的小球,从离桌面高H处自由落下,不计空气阻力,假设桌面处的重力势能为零,关于重力势能的说法正确的是( )| A. | 重力势能是矢量,有正负之分 | B. | 刚开始下落时的重力势能为mg(H+h) | ||
| C. | 落地时的重力势能为零 | D. | 落地时的重力势能为-mgh |
5. 用如图所示实验能验证动量守恒定律.两块小木块A和B中间夹着一轻质弹簧,用细线捆在一起,放在光滑的水平台面上,将细线烧断,木块A、B被弹簧弹出,最后落在水平地面上落地点与平台边缘的水平距离分别为lA=1m,lB=2m,实验结果表明下列说法正确的是( )
用如图所示实验能验证动量守恒定律.两块小木块A和B中间夹着一轻质弹簧,用细线捆在一起,放在光滑的水平台面上,将细线烧断,木块A、B被弹簧弹出,最后落在水平地面上落地点与平台边缘的水平距离分别为lA=1m,lB=2m,实验结果表明下列说法正确的是( )
 用如图所示实验能验证动量守恒定律.两块小木块A和B中间夹着一轻质弹簧,用细线捆在一起,放在光滑的水平台面上,将细线烧断,木块A、B被弹簧弹出,最后落在水平地面上落地点与平台边缘的水平距离分别为lA=1m,lB=2m,实验结果表明下列说法正确的是( )
用如图所示实验能验证动量守恒定律.两块小木块A和B中间夹着一轻质弹簧,用细线捆在一起,放在光滑的水平台面上,将细线烧断,木块A、B被弹簧弹出,最后落在水平地面上落地点与平台边缘的水平距离分别为lA=1m,lB=2m,实验结果表明下列说法正确的是( )| A. | 木块A、B离开弹簧时的速度大小之比vA:vB=1:2 | |
| B. | 木块A、B的质量之比mA:mB=1:2 | |
| C. | 弹簧对木块A、B做功之比WA:WB=1:1 | |
| D. | 木块A、B离开弹簧时的动能之比EA:EB=1:2 |
2.汽车沿平直公路做加速度大小为 0.5m/s2 的匀变速运动,那么( )
| A. | 汽车每秒钟内速度变化 0.5 m/s | |
| B. | 汽车每秒钟内加速度变化 0.5 m/s2 | |
| C. | 汽车的初速度比前 1 秒内的末速度大 0.5 m/s | |
| D. | 汽车在任意 1 s 内的末速度等于初速度的 0.5 倍 |
17.矩形导线框abcd固定在匀强磁场中,如图甲所示,磁感线的方向与导线框所在平面垂直,规定磁场的正方向垂直于纸面向里,磁感应强度B随时间t变化的规律如图乙所示,则( )


| A. | 在0~t1时间内,导线框中电流的方向为abcda | |
| B. | 在0~t1时间内,导线框中电流越来越小 | |
| C. | 在t1~t2时间内,导线框中电流保持不变 | |
| D. | 在t1~t2时间内,导线框bc边受到安培力大小保持不变 |
 在“研究匀变速直线运动”的实验中,得到的一条纸带如图所示,纸带上每相邻的两计数点间的时间间隔均为0.1s,测得A到B和B到C的距离分别为5.60cm和8.62cm,则物体的加速度大小为3.02m/s2,B点对应的速度大小为0.711 m/s.
在“研究匀变速直线运动”的实验中,得到的一条纸带如图所示,纸带上每相邻的两计数点间的时间间隔均为0.1s,测得A到B和B到C的距离分别为5.60cm和8.62cm,则物体的加速度大小为3.02m/s2,B点对应的速度大小为0.711 m/s.