题目内容
12. 一透明半圆柱的横截面如图所示,圆心为O,一束光线在横截面内从C点沿垂直于直径AB的方向入射,在半圆柱内沿图示路径传播,最后从E点射出半圆柱.已知圆半径为R=0.30m,半圆柱折射率为n=2.0,∠AOC=30°,真空中的光速为c=3.0×108m/s.求光线在半圆柱内沿图示C→D→E路径传播的时间(结果保留两位有效数字).
一透明半圆柱的横截面如图所示,圆心为O,一束光线在横截面内从C点沿垂直于直径AB的方向入射,在半圆柱内沿图示路径传播,最后从E点射出半圆柱.已知圆半径为R=0.30m,半圆柱折射率为n=2.0,∠AOC=30°,真空中的光速为c=3.0×108m/s.求光线在半圆柱内沿图示C→D→E路径传播的时间(结果保留两位有效数字).
分析 先根据几何关系求出光在C点的入射角.由折射定律求折射角.根据光在D点的入射角与临界角的大小,可判断出光在D点发生了全反射,由对称性作出光路图.由几何知识求出C→D→E路径的长度,由v=$\frac{c}{n}$求出光在半圆柱体中的传播速度大小,即可由运动学公式求出传播时间.
解答 解:光线在C点的入射角:i=90°-∠AOC=90°-30°=60°
设折射角∠OCD=r,由折射定律得:sinr=$\frac{sini}{n}$
解得:sinr=$\frac{\sqrt{3}}{4}$
可知r<30°,则∠DCP=θ>30°,sinθ>$\frac{1}{n}$,故光线在AB面上发生全反射.
作C点关于AB的对称点P,连接PC、OP、OE,则∠OPD=∠OED=r
故光线在E点将折射到空气中,光在透明体内走过的路程为:CD+DE=PE=2Rcosr
光在透明体中传播速度为:v=$\frac{c}{n}$
所求时间为:t=$\frac{CD+DE}{v}$
联立解得:t=$\sqrt{13}$×10-9s≈3.6×10-9s
答:光线在半圆柱内沿图示C→D→E路径传播的时间是3.6×10-9s.
点评 解决本题的关键利用反射的对称性作出光路图,由几何知识求有关的角度和距离,再由结合光学知识,如折射定律、v=$\frac{c}{n}$、sinC=$\frac{1}{n}$进行研究.

练习册系列答案
相关题目
3.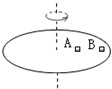 如图所示,两个质量均为m的小木块A和B(可视为质点)放在水平圆盘上,A与转轴的距离为L,B与转轴的距离为2L.木块与圆盘的最大静摩擦力为木块所受重力的k倍,重力加速度大小为g.若圆盘从静止开始绕转轴缓慢地加速转动,用ω表示圆盘转动的角速度,下列说法正确的是( )
如图所示,两个质量均为m的小木块A和B(可视为质点)放在水平圆盘上,A与转轴的距离为L,B与转轴的距离为2L.木块与圆盘的最大静摩擦力为木块所受重力的k倍,重力加速度大小为g.若圆盘从静止开始绕转轴缓慢地加速转动,用ω表示圆盘转动的角速度,下列说法正确的是( )
 如图所示,两个质量均为m的小木块A和B(可视为质点)放在水平圆盘上,A与转轴的距离为L,B与转轴的距离为2L.木块与圆盘的最大静摩擦力为木块所受重力的k倍,重力加速度大小为g.若圆盘从静止开始绕转轴缓慢地加速转动,用ω表示圆盘转动的角速度,下列说法正确的是( )
如图所示,两个质量均为m的小木块A和B(可视为质点)放在水平圆盘上,A与转轴的距离为L,B与转轴的距离为2L.木块与圆盘的最大静摩擦力为木块所受重力的k倍,重力加速度大小为g.若圆盘从静止开始绕转轴缓慢地加速转动,用ω表示圆盘转动的角速度,下列说法正确的是( )| A. | B一定比A先滑动 | |
| B. | A、B所受静摩擦力始终相等 | |
| C. | ω=$\sqrt{\frac{kg}{2L}}$是B开始滑动的临界角速度 | |
| D. | 当ω=$\sqrt{\frac{2kg}{3L}}$时,A所受的摩擦力大小为kmg |
7.以下说法正确的是( )
| A. | 在绝对光滑的水平冰面上,汽车可以转弯 | |
| B. | 火车转弯速率小于规定的数值时,内轨受的压力会增大 | |
| C. | 飞机在空中沿半径为R的水平圆周盘旋时,飞机的翅膀一定处于倾斜状态 | |
| D. | 汽车转弯时需要的向心力是司机转动方向盘所提供的力 |
2.汽车沿平直公路做加速度大小为 0.5m/s2 的匀变速运动,那么( )
| A. | 汽车每秒钟内速度变化 0.5 m/s | |
| B. | 汽车每秒钟内加速度变化 0.5 m/s2 | |
| C. | 汽车的初速度比前 1 秒内的末速度大 0.5 m/s | |
| D. | 汽车在任意 1 s 内的末速度等于初速度的 0.5 倍 |
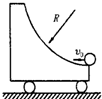 如图所示,在光滑的水平面上放置一质量为m的小车,小车上有一半径为R的$\frac{1}{4}$光滑的弧形轨道,设有一质量为m的小球,以v0的速度,方向水平向左沿圆弧轨道向上滑动,达到某一高度h后,又沿轨道下滑,试分析:
如图所示,在光滑的水平面上放置一质量为m的小车,小车上有一半径为R的$\frac{1}{4}$光滑的弧形轨道,设有一质量为m的小球,以v0的速度,方向水平向左沿圆弧轨道向上滑动,达到某一高度h后,又沿轨道下滑,试分析:
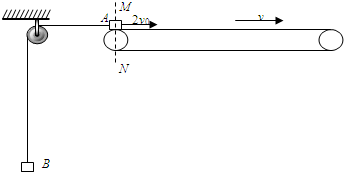
 在“研究匀变速直线运动”的实验中,得到的一条纸带如图所示,纸带上每相邻的两计数点间的时间间隔均为0.1s,测得A到B和B到C的距离分别为5.60cm和8.62cm,则物体的加速度大小为3.02m/s2,B点对应的速度大小为0.711 m/s.
在“研究匀变速直线运动”的实验中,得到的一条纸带如图所示,纸带上每相邻的两计数点间的时间间隔均为0.1s,测得A到B和B到C的距离分别为5.60cm和8.62cm,则物体的加速度大小为3.02m/s2,B点对应的速度大小为0.711 m/s.