题目内容
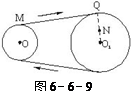
如图6-6-9所示,O、O1为两个皮带轮,O轮的半径为r,O1轮的半径为R,且R>r,M点为O轮边缘上的一点,N点为O1轮上的任意一点,当皮带轮转动时(设转动过程中不打滑),则( )

| A.M点的向心加速度一定大于N点的向心加速度 |
| B.M点的向心加速度一定等于N点的向心加速度 |
| C.M点的向心加速度可能小于N点的向心加速度 |
| D.M点的向心加速度可能等于N点的向心加速度 |
A
因为两轮的转动是通过皮带传动的,而且皮带在传动过程中不打滑,故两轮边缘各点的线速度大小一定相等。在大轮边缘上任取一点Q,因为R>r,所以由a=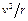 可知,aQ<aM,再比较Q、N两点的向心加速度的大小,因为Q、N是在同一轮上的两点,所以角速度ω相等。又因为RQ>RN,则由a=ω2r可知,aQ>aN,综上可见,aM>aN,因此A选项正确。
可知,aQ<aM,再比较Q、N两点的向心加速度的大小,因为Q、N是在同一轮上的两点,所以角速度ω相等。又因为RQ>RN,则由a=ω2r可知,aQ>aN,综上可见,aM>aN,因此A选项正确。
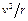 可知,aQ<aM,再比较Q、N两点的向心加速度的大小,因为Q、N是在同一轮上的两点,所以角速度ω相等。又因为RQ>RN,则由a=ω2r可知,aQ>aN,综上可见,aM>aN,因此A选项正确。
可知,aQ<aM,再比较Q、N两点的向心加速度的大小,因为Q、N是在同一轮上的两点,所以角速度ω相等。又因为RQ>RN,则由a=ω2r可知,aQ>aN,综上可见,aM>aN,因此A选项正确。
练习册系列答案
相关题目

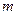 的小球连接在质量可忽略的不可伸长的柔软细线上,将细线的另一端与一竖直的光滑细圆杆的顶端相连接,并将细线绕紧在杆顶上,直至小球与圆杆相碰,此时放开小球,细线开始反向旋转释放,求细线释放完后,杆与细线的夹角
的小球连接在质量可忽略的不可伸长的柔软细线上,将细线的另一端与一竖直的光滑细圆杆的顶端相连接,并将细线绕紧在杆顶上,直至小球与圆杆相碰,此时放开小球,细线开始反向旋转释放,求细线释放完后,杆与细线的夹角 。
。
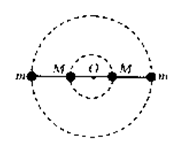
 在同一水平面上,相互平行,相距为d,两轮均以角速度
在同一水平面上,相互平行,相距为d,两轮均以角速度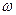 逆时针方向匀速转动。将一长木板置于两轮上,当木板的重心位于右轮正
逆时针方向匀速转动。将一长木板置于两轮上,当木板的重心位于右轮正 上方时,木板与两轮间已不现有相对滑动。若木板的长度L>2d,则木板的重心由右轮正上方移到左轮正上方所需的时间是( )
上方时,木板与两轮间已不现有相对滑动。若木板的长度L>2d,则木板的重心由右轮正上方移到左轮正上方所需的时间是( )
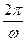
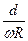
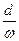
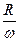
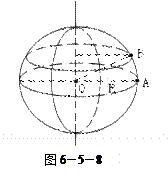
 半径的两倍。A、B分别为大小轮边缘上的点,C为大轮上一条半径的中点,则下列关系正确的是( )
半径的两倍。A、B分别为大小轮边缘上的点,C为大轮上一条半径的中点,则下列关系正确的是( )

 B.
B.

