题目内容
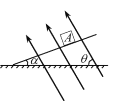
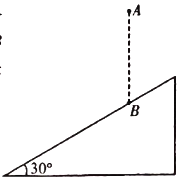
【题目】有一种用于电子显示屏的发光二极管，其管芯的发光区域是直径为D的圆面，P为O点正上方球面上的一点，发光二极管中半球体介质的半径为R，如图所示.
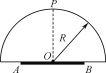
①若介质的折射率n1＝
，真空中光速为c，求光从A点沿直线传播到P点的时间t；
②为使从发光面AB发出的光在球面上都不发生全反射，介质的折射率n应满足什么条件？
【答案】①t＝
.②n<
【解析】
由几何关系求解光从A点传播到P点的距离，根据v=c/n求解速度，根据t=x/v求解时间；考虑临界情况，从A点或B点垂直于圆盘射出的光射到球面的入射角最大，然后结合公式n=1/sinC 进行分析即可．
①光在介质中的传播速度v＝
则此光从A点传播到P点的时间
解得t＝.
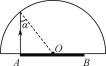
②从A或B点垂直于圆盘射出的光射到球面的入射角最大(设为α)，则
sinα＝
设光发生全反射的临界角为C，则sinC＝
不发生全反射应满足sinα<sinC
解得n<.
练习册系列答案
优学名师名题系列答案
相关题目
