题目内容
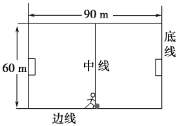
【题目】某次足球比赛中,攻方使用“边路突破,下底传中”的战术。如图,足球场长90m、宽60m.前锋甲在中线处将足球沿边线向前踢出,足球的运动可视为在地面上做匀减速直线运动,其初速度v0=12m/s,加速度大小a0=2m/s2.
(1)甲踢出足球的同时沿边线向前追赶足球,设他做初速为零、加速度a1=2m/s2的匀加速直线运动,能达到的最大速度vm=8m/s.求他追上足球的最短时间.
(2)若甲追上足球的瞬间将足球以某速度v沿边线向前踢出,足球仍以a0在地面上做匀减速直线运动;同时,甲的速度瞬间变为v1=6 m/s,紧接着他做匀速直线运动向前追赶足球,恰能在底线处追上足球传中,求v的大小.
【答案】(1)t=6.5s (2)v=7.5m/s
【解析】
(1)根据速度时间公式求出运动员达到最大速度的时间和位移,然后运动员做匀速直线运动,结合位移关系求出追及的时间.
(2)结合运动员和足球的位移关系,运用运动学公式求出前锋队员在底线追上足球时的速度.
(1)已知甲的加速度为![]() ,最大速度为
,最大速度为![]() ,甲做匀加速运动达到最大速度的时间和位移分别为:
,甲做匀加速运动达到最大速度的时间和位移分别为:![]()
![]()
之后甲做匀速直线运动,到足球停止运动时,其位移x2=vm(t1-t0)=8×2m=16m
由于x1+x2 < x0,故足球停止运动时,甲没有追上足球
甲继续以最大速度匀速运动追赶足球,则x0-(x1+x2)=vmt2
联立得:t2=0.5s
甲追上足球的时间t=t0+t2=6.5s
(2)足球距底线的距离x2=45-x0=9m
设甲运动到底线的时间为t3,则x2=v1t3
足球在t3时间内发生的位移![]()
联立解得:v=7.5m/s

练习册系列答案
相关题目