题目内容
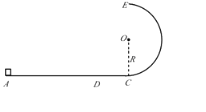
【题目】如图所示,一足够长的水平轨道ADC由粗糙部分AD和光滑部分DC组成,粗糙部分的动摩擦因数μ=0.5,半径为R=1m的光滑竖直半圆轨道CE与水平轨道相切。一质量m=0.5kg的小物块以初速度v0从D点向右运动冲上半圆轨道,小物块至最高点E时,其对轨道的压力25N,重力加速度g取10m/s2,求:
(1)小物块在最高点时受到的向心力大小;
(2)小物块的初速度v0;
(3)改变小物块在水平面AC运动的初始位置,若要使小物块能通过半圆轨道最高点,则小物块初始位置与D点的距离x必须满足什么条件?
【答案】(1)小物块在最高点时受到的向心力大小是30N;(2)小物块的初速度是10m/s;(3)小物块初始位置与D点的距离x必须满足x≤5m。
【解析】
(1)小物块在最高点时受重力和轨道对小球的弹力N,由牛顿第三定律知轨道对小球的弹力N=25N,所以向心力为F=mg+N=30N
(2)设在最高点的速度为v1,由牛顿第二定律得:mg+N=m![]()
从D到最高点的过程由动能定理得:-mg2R=![]() -
-![]()
联立解得:v0=10m/s
(3)设物块通过半圆轨道最高点为v,由牛顿第二定律得:m![]() ≥mg,即v≥
≥mg,即v≥![]()
从释放点到最高点的过程由动能定理得:-μmgx-mg2R=![]() -
-![]()
联立解得:x≤5m

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目