题目内容
7. 我国将于2015年发射空间站,设该空间站体积很大,宇航员可以在里面进行多项体育活动,一宇航员在站内玩垒球(万有引力可以忽略不计),上半侧为匀强电场,下半侧为匀强磁场,中间为分界面,电场与分界面垂直,磁场垂直纸面向里,电场强度为E=100V/m,宇航员位于电场一侧距分界面为h=3m的P点,po垂直于分界面,D位于o点右侧,垒球质量为m=0.1kg,带电量为q=-0.05C,该宇航员从P点以初速度v0=10m/s平行于界面投出垒球,要垒球第一次通过界面就击中D点,且能回到P点.求:
我国将于2015年发射空间站,设该空间站体积很大,宇航员可以在里面进行多项体育活动,一宇航员在站内玩垒球(万有引力可以忽略不计),上半侧为匀强电场,下半侧为匀强磁场,中间为分界面,电场与分界面垂直,磁场垂直纸面向里,电场强度为E=100V/m,宇航员位于电场一侧距分界面为h=3m的P点,po垂直于分界面,D位于o点右侧,垒球质量为m=0.1kg,带电量为q=-0.05C,该宇航员从P点以初速度v0=10m/s平行于界面投出垒球,要垒球第一次通过界面就击中D点,且能回到P点.求:(1)OD之间的距离d.
(2)垒球从抛出第一次回到P点的时间t.(计算结果保留三位有效数字)
分析 (1)垒球在电场中的运动为平抛运动,由平抛运动的规律可得出OD间的距离及在电场中运动的时间;
(2)垒球在磁场中做圆周运动,由几何关系可得出粒子半径的表达式,则由牛顿第二定律可求得B,再由转过的角度可求得在磁场中的转动时间,则可求得总时间.
解答 解:(1)设垒球在电场中运动的加速度大小为a,时间为t1,OD=d,
垒球在电场中做类平抛运动,
水平方向:d=v1t,
竖直方向:h=$\frac{1}{2}$at12=$\frac{1}{2}$$\frac{qE}{m}$t12,
解得:a=50m/s2,t1=$\frac{\sqrt{3}}{5}$s,d=2$\sqrt{3}$m=3.46m,
即O、D两点之间的距离为3.46m.
(2)垒球的运动轨迹如图所示.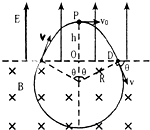
由图可知,tanθ=$\frac{a{t}_{1}}{{v}_{1}}$=$\sqrt{3}$,
速度大小为:v=$\frac{{v}_{1}}{cosθ}$=20m/s,
设垒球作匀速圆周运动半径为R,磁感应强度大小为B,则R=$\frac{d}{sinθ}$=4m,
根据牛顿第二定律,有:qvB=m$\frac{{v}^{2}}{R}$,
解得:B=$\frac{mv}{qR}$=10T,
垒球在磁场中运动的时间为:t2=$\frac{α}{360°}$T=$\frac{360°-2×60°}{360°}$×$\frac{2πm}{qB}$=$\frac{4π}{15}$s,
垒球从抛出到第一次回到P点的时间为:t=2t1+t2=$\frac{6\sqrt{3}+4π}{15}$s=1.53s;
答:(1)OD之间的距离3.46m.
(2)垒球从抛出到第一次回到P点的时间1.53s.
点评 带电粒子在磁场中的转动问题要注意通过分析画出相应的运动图象,由图象即可得出半径关系,再由洛仑兹力充当向心力即可求出待求的磁感应强度,即半径是此类题型的突破口.

 阅读快车系列答案
阅读快车系列答案 如图所示,质量为m的物体B叠放在物体A上,A的上表面水平.A、B一起沿着倾角为θ的固定光滑斜面由静止开始下滑,在A、B一起沿光滑斜面下滑的过程中( )
如图所示,质量为m的物体B叠放在物体A上,A的上表面水平.A、B一起沿着倾角为θ的固定光滑斜面由静止开始下滑,在A、B一起沿光滑斜面下滑的过程中( )| A. | B受到的支持力为mgsin2θ | |
| B. | B受到的静摩擦力方向水平向左 | |
| C. | A对B的作用力为mgsinθ,方向沿斜面向下 | |
| D. | B物体的机械能守恒 |
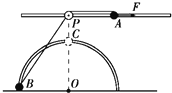 如图所示,在距水平地面高为0.4m处,水平固定一根长直光滑杆,在杆上P点固定一定滑轮,滑轮可绕水平轴无摩擦转动,在P点的右边,杆上套有一质量m=2kg的小球A.半径R=0.3m的光滑半圆形细轨道,竖直地固定在地上,其圆心O在P点的正下方,在轨道上套有一质量也为m=2kg的小球B.用一条不可伸长的柔软细绳,通过定滑轮将两小球连接起来.杆和半圆形轨道在同一竖直面内,两小球均可看做质点,不计滑大小的影响,且细绳刚好没有张力,g取0m/s2.现给小球A一个水平向右的恒力F=55N.以下说法正确的是( )
如图所示,在距水平地面高为0.4m处,水平固定一根长直光滑杆,在杆上P点固定一定滑轮,滑轮可绕水平轴无摩擦转动,在P点的右边,杆上套有一质量m=2kg的小球A.半径R=0.3m的光滑半圆形细轨道,竖直地固定在地上,其圆心O在P点的正下方,在轨道上套有一质量也为m=2kg的小球B.用一条不可伸长的柔软细绳,通过定滑轮将两小球连接起来.杆和半圆形轨道在同一竖直面内,两小球均可看做质点,不计滑大小的影响,且细绳刚好没有张力,g取0m/s2.现给小球A一个水平向右的恒力F=55N.以下说法正确的是( )| A. | 把小球B从地面拉到P点正下方C点过程中,力F做的功WF=16.5J | |
| B. | 当细绳与圆形轨道相切时,小球B与小球A速度大小相等 | |
| C. | 把小球B从地面拉到P点正下方C点时,小球A速度的大小v=3$\sqrt{2}$m/s | |
| D. | 把小球B从地面拉到P点正下方C点时,小球B速度的大小v=4m/s |
| A. | 位移大小可能为3m | B. | 位移大小可能大于3m | ||
| C. | 加速度大小可能为6m/s2 | D. | 加速度的大小可能大于6m/s2 |
| A. | 可能的渡河时间为$\frac{d}{{v}_{2}}$ | |
| B. | 可能的最短渡河位移为d | |
| C. | 只有当船头垂直河岸渡河时,渡河时间才和水速无关 | |
| D. | 不管船头与河岸夹角是多少,渡河时间和水速均无关 |
 2014年3月8日凌晨马航客机失联后,北京卫星测控中心紧急调动海洋、风云、高分、遥感4个型号近10颗卫星,为海面搜救提供技术支持,特别是“高分一号”突破了空间分辨率、多光谱与大覆盖面积相结合的多项关键核心技术.如图所示为“高分一号”与北斗导航系统两颗工作卫星在太空同一轨道面内运动的示意图,北斗导航系统中两颗卫星“B1”和“B2”以及“高分一号”均可认为绕地心O做匀速圆周运动,卫星“B1”和“B2”的轨道半径均为r;某时刻北斗导航系统两颗工作卫星分别位于轨道上的M、N两位置,两者轨道半径夹角为600,“高分一号”在C位置.卫星均顺时针运行,地球表面的重力加速度为g,地球半径为R,则下列说法正确的是( )
2014年3月8日凌晨马航客机失联后,北京卫星测控中心紧急调动海洋、风云、高分、遥感4个型号近10颗卫星,为海面搜救提供技术支持,特别是“高分一号”突破了空间分辨率、多光谱与大覆盖面积相结合的多项关键核心技术.如图所示为“高分一号”与北斗导航系统两颗工作卫星在太空同一轨道面内运动的示意图,北斗导航系统中两颗卫星“B1”和“B2”以及“高分一号”均可认为绕地心O做匀速圆周运动,卫星“B1”和“B2”的轨道半径均为r;某时刻北斗导航系统两颗工作卫星分别位于轨道上的M、N两位置,两者轨道半径夹角为600,“高分一号”在C位置.卫星均顺时针运行,地球表面的重力加速度为g,地球半径为R,则下列说法正确的是( )| A. | 北斗导航卫星“B1”和“B2”的加速度大小为$\frac{r}{R}$g | |
| B. | 如果要调动“高分一号”卫星尽快到达N位置的下方,必须使其加速 | |
| C. | 卫星B1由M运动到N所需要的时间为t=$\frac{πr}{3R}\sqrt{\frac{r}{R}}$. | |
| D. | 若“高分一号”所在高度处有稀薄气体,则运行一段时间后,其机械能会增大 |
 如图所示,xOy坐标平面中的直角三角形ACD区域,AC与CD长度均为l,且A、C、D均位于坐标轴上,区域内有垂直于坐标平面向里的匀强磁场,磁感应强度大小为B.坐标原点O处有一粒子源,粒子源能够从O点沿x轴正方向发射出大量带正电的同种粒子,不计粒子重力及粒子间相互作用,粒子的比荷为$\frac{q}{m}$,发现恰好所有粒子都不能从AC边射出,求这些粒子中速度的最大值.
如图所示,xOy坐标平面中的直角三角形ACD区域,AC与CD长度均为l,且A、C、D均位于坐标轴上,区域内有垂直于坐标平面向里的匀强磁场,磁感应强度大小为B.坐标原点O处有一粒子源,粒子源能够从O点沿x轴正方向发射出大量带正电的同种粒子,不计粒子重力及粒子间相互作用,粒子的比荷为$\frac{q}{m}$,发现恰好所有粒子都不能从AC边射出,求这些粒子中速度的最大值.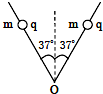 如图所示,竖直面内有两光滑固定的绝缘细棒,与竖直方向夹角都是37°,两棒上各穿有带正电的小球,两球处于静止状态.两小球带电量都是q=2.0×10-7库仑,质量都是m=0.4克,求:
如图所示,竖直面内有两光滑固定的绝缘细棒,与竖直方向夹角都是37°,两棒上各穿有带正电的小球,两球处于静止状态.两小球带电量都是q=2.0×10-7库仑,质量都是m=0.4克,求: