题目内容
17. 如图所示,竖直面内有两光滑固定的绝缘细棒,与竖直方向夹角都是37°,两棒上各穿有带正电的小球,两球处于静止状态.两小球带电量都是q=2.0×10-7库仑,质量都是m=0.4克,求:
如图所示,竖直面内有两光滑固定的绝缘细棒,与竖直方向夹角都是37°,两棒上各穿有带正电的小球,两球处于静止状态.两小球带电量都是q=2.0×10-7库仑,质量都是m=0.4克,求:(1)每个小球所受到的棒的支持力大小;
(2)两小球间的距离r.(g=10m/s2,k=9×109N•m2/C2,sin37°=0.6,cos37°=0.8)
分析 对其中一个小球受力分析,由平衡条件求出小球受到的库仑力,然后由库仑定律求出两球间的距离r.
解答 解:(1)以其中一个小球为研究对象受力分析,运用合成法,如图:
由几何知识得:
N=$\frac{mg}{sin37°}$=$\frac{0.4×1{0}^{-3}}{0.6}$≈6.7×10-2N
(2)而F=mgtan53°=$\frac{4}{3}$mg
根据库仑定律:F=k$\frac{{q}^{2}}{{r}^{2}}$
得:r=$\sqrt{\frac{3k{q}^{2}}{4mg}}$
代入数据,解得:r≈0.26m
答:(1)每个小球所受到的棒的支持力大小6.7×10-2N;
(2)两小球间的距离0.26m.
点评 本题借助库仑力考查了平衡条件的应用,能正确的受力分析并结合合成法求力的大小是力学部分的基本功,同时掌握库仑定律的内容.

练习册系列答案
相关题目
2. 位于水平面上的物体在水平恒力F1作用下,做速度为v1的匀速运动;若作用力变为斜向下的恒力F2,物体做速度为v2的匀速运动,且F1与F2功率相同.则有( )
位于水平面上的物体在水平恒力F1作用下,做速度为v1的匀速运动;若作用力变为斜向下的恒力F2,物体做速度为v2的匀速运动,且F1与F2功率相同.则有( )
 位于水平面上的物体在水平恒力F1作用下,做速度为v1的匀速运动;若作用力变为斜向下的恒力F2,物体做速度为v2的匀速运动,且F1与F2功率相同.则有( )
位于水平面上的物体在水平恒力F1作用下,做速度为v1的匀速运动;若作用力变为斜向下的恒力F2,物体做速度为v2的匀速运动,且F1与F2功率相同.则有( )| A. | F2=F1,v1<v2 | B. | F2=F1,v1>v2 | C. | F2<F1,v1<v2 | D. | F2>F1,v1>v2 |
9.物体从静止开始作匀加速直线运动,第3s内通过的位移是3m,则( )
| A. | 第3s内的平均速度是1m/s | B. | 物体的加速度是1.2m/s2 | ||
| C. | 前3s内的位移是6m | D. | 第3s初的速度是3.6m/s |
6. 如图所示,调整可变电阻R的大小,使得三灯泡的功率相同,设三个灯泡的电阻分别为L1、L2、L3,比较它们的大小( )
如图所示,调整可变电阻R的大小,使得三灯泡的功率相同,设三个灯泡的电阻分别为L1、L2、L3,比较它们的大小( )
 如图所示,调整可变电阻R的大小,使得三灯泡的功率相同,设三个灯泡的电阻分别为L1、L2、L3,比较它们的大小( )
如图所示,调整可变电阻R的大小,使得三灯泡的功率相同,设三个灯泡的电阻分别为L1、L2、L3,比较它们的大小( )| A. | L1=L2=L3 | B. | L1<L2=L3 | ||
| C. | L3>L1>L2 | D. | 由于R的大小未知,无法确定 |
7.某金属导线的电阻为R,现将它均匀拉长到半径为原来的一半,那么该导线的电阻变为( )
| A. | 2R | B. | 4R | C. | 8R | D. | 16R |
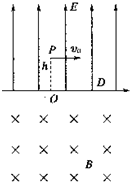 我国将于2015年发射空间站,设该空间站体积很大,宇航员可以在里面进行多项体育活动,一宇航员在站内玩垒球(万有引力可以忽略不计),上半侧为匀强电场,下半侧为匀强磁场,中间为分界面,电场与分界面垂直,磁场垂直纸面向里,电场强度为E=100V/m,宇航员位于电场一侧距分界面为h=3m的P点,po垂直于分界面,D位于o点右侧,垒球质量为m=0.1kg,带电量为q=-0.05C,该宇航员从P点以初速度v0=10m/s平行于界面投出垒球,要垒球第一次通过界面就击中D点,且能回到P点.求:
我国将于2015年发射空间站,设该空间站体积很大,宇航员可以在里面进行多项体育活动,一宇航员在站内玩垒球(万有引力可以忽略不计),上半侧为匀强电场,下半侧为匀强磁场,中间为分界面,电场与分界面垂直,磁场垂直纸面向里,电场强度为E=100V/m,宇航员位于电场一侧距分界面为h=3m的P点,po垂直于分界面,D位于o点右侧,垒球质量为m=0.1kg,带电量为q=-0.05C,该宇航员从P点以初速度v0=10m/s平行于界面投出垒球,要垒球第一次通过界面就击中D点,且能回到P点.求: