题目内容
12．
如图所示，xOy坐标平面中的直角三角形ACD区域，AC与CD长度均为l，且A、C、D均位于坐标轴上，区域内有垂直于坐标平面向里的匀强磁场，磁感应强度大小为B．坐标原点O处有一粒子源，粒子源能够从O点沿x轴正方向发射出大量带正电的同种粒子，不计粒子重力及粒子间相互作用，粒子的比荷为$\frac{q}{m}$，发现恰好所有粒子都不能从AC边射出，求这些粒子中速度的最大值．
分析 粒子从O点沿着+x方向射入磁场，洛伦兹力向上，圆心在O点的正上方，画出临界轨迹，结合几何关系得到轨道半径，根据牛顿第二定律列式求解最大速度．
解答 
解：当粒子以最大的可能速度沿着x轴正方向进入磁场时，轨迹如图所示，要使所有粒子都不能从AC边射出，则最大轨迹圆恰好AC、CD边相切．
故由几何关系可得带电粒子运动的轨道半径R=$\frac{（2-\sqrt{2}）l}{2}$
又：qvB=m$\frac{{v}^{2}}{R}$
解得这些粒子中速度的最大值为：v=$\frac{qBl（2-\sqrt{2}）}{2m}$
答：这些粒子中速度的最大值为$\frac{qBl（2-\sqrt{2}）}{2m}$．
点评 本题关键是画出运动轨迹，得到临界轨迹的半径；明确粒子做匀速圆周运动，洛伦兹力提供向心力，根据牛顿第二定律列式求解即可．
练习册系列答案
相关题目
3．
如图所示，虚线框内为一加速度计的原理图，把它放在沿水平方向做加速运动的物体上，使AB杆沿物体加速度方向放置，可根据电压表的示数测得物体加速度．AB是一根光滑细杆，装有滑键P的滑块m可沿AB杆自由滑动，滑块右侧通过一根弹簧与B端相拴接，R是一根长为L=1m，粗细均匀的电阻丝，理想电压表通过松弛的导线与滑键P相连接（保证滑块m能在细杆上自由滑动），电源电源恒定为U，弹簧劲度系数k=100N/m，滑块及滑键质量为m=2kg，当装置静止时，电压表示数为$\frac{U}{2}$，P始终与电阻丝R保持良好接触．则当电压表示数为$\frac{U}{3}$时，物体加速度为（ ）
如图所示，虚线框内为一加速度计的原理图，把它放在沿水平方向做加速运动的物体上，使AB杆沿物体加速度方向放置，可根据电压表的示数测得物体加速度．AB是一根光滑细杆，装有滑键P的滑块m可沿AB杆自由滑动，滑块右侧通过一根弹簧与B端相拴接，R是一根长为L=1m，粗细均匀的电阻丝，理想电压表通过松弛的导线与滑键P相连接（保证滑块m能在细杆上自由滑动），电源电源恒定为U，弹簧劲度系数k=100N/m，滑块及滑键质量为m=2kg，当装置静止时，电压表示数为$\frac{U}{2}$，P始终与电阻丝R保持良好接触．则当电压表示数为$\frac{U}{3}$时，物体加速度为（ ）| A． | 8.33 m/s2，方向向左 | B． | 8.33m/s2，方向向右 | ||
| C． | 16.67m/s2，方向向左 | D． | 16.67m/s2，方向向右 |
4．下列各量中，与试探电荷无关的量是（ ）
| A． | 电场强度E | B． | 静电力F | C． | 电势差U | D． | 电场做的功W |
1．电路如图所示，当滑动变阻器的触头P向上滑动时，则（ ）
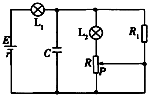
| A． | 电源的总功率变小 | B． | 电容器贮存的电量变小 | ||
| C． | 灯L1变亮 | D． | 灯L2变暗 |
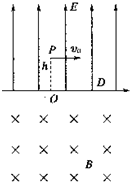我国将于2015年发射空间站，设该空间站体积很大，宇航员可以在里面进行多项体育活动，一宇航员在站内玩垒球（万有引力可以忽略不计），上半侧为匀强电场，下半侧为匀强磁场，中间为分界面，电场与分界面垂直，磁场垂直纸面向里，电场强度为E=100V/m，宇航员位于电场一侧距分界面为h=3m的P点，po垂直于分界面，D位于o点右侧，垒球质量为m=0.1kg，带电量为q=-0.05C，该宇航员从P点以初速度v0=10m/s平行于界面投出垒球，要垒球第一次通过界面就击中D点，且能回到P点．求：
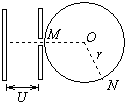如图所示，离子源从小孔发射出带电量为e的正离子（初速度可忽略），在加速电压U的作用下，沿MO方向进入匀强磁场中，磁场限制在以O点为圆心，半径为r的区域内，磁感应强度为B，方向垂直纸面向外，离子从N点射出，已知∠MON=120°，则正离子质量为$\frac{3e{B}^{2}{r}^{2}}{2U}$，正离子通过磁场所需时间为$\frac{\sqrt{3}πr}{3v}$．
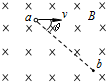如图所示，在磁感应强度为B、方向垂直纸面向里的匀强磁场中，一质量为m、电量为e的电子，从a点沿垂直磁感线方向以初速度v开始运动，经一段时间t后经过b点，ab连线与初速度的夹角为θ，则t=$\frac{2θm}{eB}$．
1．
如图所示，一小球从距竖直弹簧一定高度静止释放，与弹簧接触后压缩弹簧到最低点（设此点小球的重力势能为0）．在此过程中，小球重力势能和动能的最大值分别为Ep和Ek，弹簧弹性势能的最大值为E′p则它们之间的关系为（ ）
如图所示，一小球从距竖直弹簧一定高度静止释放，与弹簧接触后压缩弹簧到最低点（设此点小球的重力势能为0）．在此过程中，小球重力势能和动能的最大值分别为Ep和Ek，弹簧弹性势能的最大值为E′p则它们之间的关系为（ ）| A． | Ep=E′p＞Ek | B． | Ep＞Ek＞E′p | C． | Ep=Ek+E′p | D． | Ep+Ek=E′p |
2．
位于水平面上的物体在水平恒力F1作用下，做速度为v1的匀速运动；若作用力变为斜向下的恒力F2，物体做速度为v2的匀速运动，且F1与F2功率相同．则有（ ）
位于水平面上的物体在水平恒力F1作用下，做速度为v1的匀速运动；若作用力变为斜向下的恒力F2，物体做速度为v2的匀速运动，且F1与F2功率相同．则有（ ）| A． | F2=F1，v1＜v2 | B． | F2=F1，v1＞v2 | C． | F2＜F1，v1＜v2 | D． | F2＞F1，v1＞v2 |