题目内容
如图所示为三块质量均为m，长度均为L的木块。木块1和木块2重叠放置在光滑的水平桌面上，木块3沿光滑水平桌面运动并与叠放在下面的木块2发生碰撞后粘合在一起，如果要求碰后原来叠放在上面的木块1完全移到木块3上，并且不会从木块3上掉下，木块3碰撞前的动能应满足什么条件？设木块之间的动摩擦因数为m。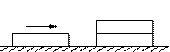
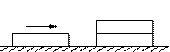
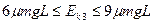
设第3块木块的初速度为V0，对于3、2两木块的系统，设碰撞后的速度为V1，据动量守恒定律得：mV0="2mV1 "
对于3、2整体与1组成的系统，设共同速度为V2，则据动量守恒定律得：
2mV1="3mV2 "
(1)第1块木块恰好运动到第3块上，首尾相齐，则据能量守恒有：
联立方程得：Ek3="6μmgL "
(2)第1块运动到第3块木块上，恰好不掉下，据能量守恒定律得：
联立方程得：Ek3=9μmgL
故：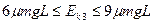
对于3、2整体与1组成的系统，设共同速度为V2，则据动量守恒定律得：
2mV1="3mV2 "
(1)第1块木块恰好运动到第3块上，首尾相齐，则据能量守恒有：
联立方程得：Ek3="6μmgL "
(2)第1块运动到第3块木块上，恰好不掉下，据能量守恒定律得：
联立方程得：Ek3=9μmgL
故：
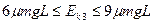
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
状元及第系列答案
同步奥数系列答案
相关题目
，式中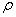
为大气的密度，v是返回舱的运动速度，S为与形状特征有关的阻力面积。当返回舱距地面高度为10km时，打开面积为1200m2的降落伞，直到速度达到8.0m/s后匀速下落。为实现软着陆（即着陆时返回舱的速度为0），当返回舱离地面1.2m时反冲发动机点火，使返回舱落地的速度减为零，返回舱此时的质量为2.7×103kg 取g=10m/s2。
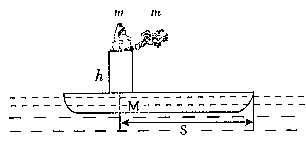
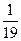m1、带电荷量为+q的金属球b用等长的绝缘轻质细线吊在天花板上，它们静止时刚好接触，并且ab接触处贴一绝缘纸、使ab碰撞过程中没有电荷转移，在PQ左侧有垂直纸面向里磁感应强度为B的匀强磁场，在PQ右侧有竖直向下的匀强电场、场强大小为E＝
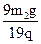。现将球b拉至细线与竖直方向成θ＝53°的位置（细线刚好拉直）自由释放，下摆后在最低点与a球发生弹性碰撞。由于电磁阻尼作用，球a将于再次碰撞前停在最低点，求经过多少次碰撞后悬挂b的细线偏离竖直方向的夹角小于37°？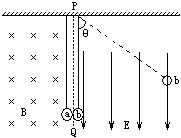
；
