题目内容
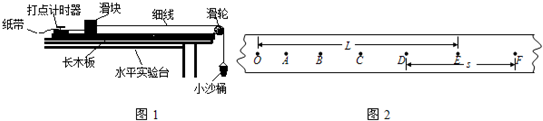
12.某学习小组的同学想要验证“动能定理”,他们在实验室组装了一套如图1装置,当滑块连接上纸带,用细线通过滑轮挂上空的小沙桶时,释放小面桶,滑块处于静止状态.如果要完成该项实验,则:(1)进行实验操作时,首先要做的步骤是平衡摩擦力.
(2)实验时释放滑块让沙桶带着滑块加速运动,用打点计时器(打点周期为T)记录其运动情况如图2纸带所示,每两点间还有4个点也未画出,现测得O到E点间的长为L,D到F点间的长为S,则E点速度大小为$\frac{S}{10T}$.若取O点的速度为v1、E点速度为v2(滑块的质量M,沙和沙桶的总质量m,且满足m<<M)那么本实验最终要验证的数学表达式为$MgL=\frac{1}{2}M{v}_{2}^{2}-\frac{1}{2}M{v}_{1}^{2}$.
分析 (1)实验要测量滑块动能的增加量和合力做的功,用沙和沙桶的总质量表示滑块受到的拉力,对滑块受力分析,受到重力、拉力、支持力和摩擦力,要使拉力等于合力,必须使重力的下滑分量等于摩擦力;
(2)由平均速度公式求解E点的速度;注意时间为5T;实验要测量滑块动能的增加量和合力做的功,求出合力的功和动能的增加量即可.
解答 解:(1)小车下滑时受到重力、细线的拉力、支持力和摩擦力,要使拉力等于合力,则应该用重力的下滑分量来平衡摩擦力,故可以将长木板的不带滑轮的一端垫高.来平衡摩擦力;
(2)由于滑块做匀加速直线运动,实验DF段的平均速度等于DF段上中点时刻E的瞬时速度,即:${v}_{E}=\overline{{v}_{DF}}=\frac{\overline{DF}}{2t}=\frac{S}{2×5T}=\frac{S}{10T}$
若取O点的速度为v1、E点速度为v2那么滑块动能的增加量:$△{E}_{k}=\frac{1}{2}M{v}_{2}^{2}-\frac{1}{2}M{v}_{1}^{2}$
滑块势能的减少量:△EP=MgL
本实验最终要验证的数学表达式为动能增加量等于重力势能的减少量,故为:$MgL=\frac{1}{2}M{v}_{2}^{2}-\frac{1}{2}M{v}_{1}^{2}$
故答案为:(1)平衡摩擦力;(2)$\frac{S}{10T}$;$MgL=\frac{1}{2}M{v}_{2}^{2}-\frac{1}{2}M{v}_{1}^{2}$
点评 本题关键是根据实验原理并结合牛顿第二定律和动能定理来确定要测量的量、实验的具体操作方法和实验误差的减小方法.要注意平均速度公式的正确应用.

练习册系列答案
相关题目
17.201年11月3日,“神州八号”飞船与“天宫一号”目标飞行器成功实施了首次交会对接.任务完成后“天宫一号”经变轨升到更高的轨道,等待与“神州九号”交会对接.变轨前和变轨完成后“天宫一号”的运行轨道均可视为圆轨道,对应的轨道半径分别为R1、R2,线速度大小分别为v1、v2,则$\frac{{V}_{1}}{{V}_{2}}$ 等于( )
| A. | $\frac{{{R}_{2}}^{2}}{{{R}_{1}}^{2}}$ | B. | $\sqrt{\frac{{{R}_{1}}^{3}}{{{R}_{2}}^{3}}}$ | C. | $\frac{{R}_{2}}{{R}_{1}}$ | D. | $\sqrt{\frac{{R}_{2}}{{R}_{1}}}$ |
18. 一质量为M,倾角为θ的楔形木块,静置在光滑水平面上,质量为m的物块,置于楔形木块的光滑斜面上.为了保持物块相对斜面静止,可用一水平力F推楔形木块,则( )
一质量为M,倾角为θ的楔形木块,静置在光滑水平面上,质量为m的物块,置于楔形木块的光滑斜面上.为了保持物块相对斜面静止,可用一水平力F推楔形木块,则( )
 一质量为M,倾角为θ的楔形木块,静置在光滑水平面上,质量为m的物块,置于楔形木块的光滑斜面上.为了保持物块相对斜面静止,可用一水平力F推楔形木块,则( )
一质量为M,倾角为θ的楔形木块,静置在光滑水平面上,质量为m的物块,置于楔形木块的光滑斜面上.为了保持物块相对斜面静止,可用一水平力F推楔形木块,则( )| A. | 楔形木块对物块的支持力为mgcosθ | B. | 楔形木块对物块的支持力为$\frac{mg}{cosθ}$ | ||
| C. | 整体的加速度为gtanθ | D. | F=(M+m)gtanθ |
7. 如图所示为质点P、Q做匀速圆周运动的向心加速度随半径变化的图线.表示质点P的图线是过原点的一条直线,表示质点Q的图线是双曲线.由图线可知( )
如图所示为质点P、Q做匀速圆周运动的向心加速度随半径变化的图线.表示质点P的图线是过原点的一条直线,表示质点Q的图线是双曲线.由图线可知( )
 如图所示为质点P、Q做匀速圆周运动的向心加速度随半径变化的图线.表示质点P的图线是过原点的一条直线,表示质点Q的图线是双曲线.由图线可知( )
如图所示为质点P、Q做匀速圆周运动的向心加速度随半径变化的图线.表示质点P的图线是过原点的一条直线,表示质点Q的图线是双曲线.由图线可知( )| A. | 质点P的线速度大小不变 | B. | 质点P的角速度大小不变 | ||
| C. | 质点Q的角速度大小不变 | D. | 质点Q的周期大小不变 |
2.某实验小组探究弹簧的劲度系数k与其长度(圈数)的关系.实验装置如图(a)所示:一均匀长弹簧竖直悬挂,7个指针P0、P1、P2、P3、P4、P5、P6分别固定在弹簧上距悬点0、10、20、30、40、50、60圈处;通过旁边竖直放置的刻度尺,可以读出指针的位置,P0指向0刻度.设弹簧下端未挂重物时,各指针的位置记为x0;挂有质量为0.100kg的砝码时,各指针的位置记为x.测量结果及部分计算结果如下表所示(n为弹簧的圈数,重力加速度取9.80m/s2).已知实验所用弹簧总圈数为60,整个弹簧的自由长度为11.88cm.
(1)将表中数据补充完整:①81.7;②0.0122.
(2)以n为横坐标,$\frac{1}{k}$为纵坐标,在图(b)给出的坐标纸上画出$\frac{1}{k}$ n图象.

(3)图(b)中画出的直线可近似认为通过原点.若从实验中所用的弹簧截取圈数为n的一段弹簧,该弹簧的劲度系数k与其圈数n的关系的表达式为k=$\frac{1.67×1{0}^{3}}{n}$N/m.
(1)将表中数据补充完整:①81.7;②0.0122.
| P1 | P2 | P3 | P4 | P5 | P6 | |
| x0(cm) | 2.04 | 4.06 | 6.06 | 8.05 | 10.03 | 12.01 |
| x(cm) | 2.64 | 5.26 | 7.81 | 10.30 | 12.93 | 15.41 |
| n | 10 | 20 | 30 | 40 | 50 | 60 |
| k(N/m) | 163 | ① | 56.0 | 43.6 | 33.8 | 28.8 |
| $\frac{1}{k}$(m/N) | 0.0061 | ② | 0.0179 | 0.0229 | 0.0296 | 0.0347 |

(3)图(b)中画出的直线可近似认为通过原点.若从实验中所用的弹簧截取圈数为n的一段弹簧,该弹簧的劲度系数k与其圈数n的关系的表达式为k=$\frac{1.67×1{0}^{3}}{n}$N/m.
 如图所示,平行金属导轨间距为50cm,固定在水平面上,一端接入电动势E=1.5V,内电阻为r=0.2Ω的电池,金属杆ab的电阻为R=2.8Ω,质量为m=5×10-2kg,与平行导轨垂直放置,其余电阻不计,金属杆处于磁感应强度为B=0.8T,方向与水平方向成60°的匀强磁场中,接通电路后,金属杆ab仍保持静止,求;(g=10m/s2)
如图所示,平行金属导轨间距为50cm,固定在水平面上,一端接入电动势E=1.5V,内电阻为r=0.2Ω的电池,金属杆ab的电阻为R=2.8Ω,质量为m=5×10-2kg,与平行导轨垂直放置,其余电阻不计,金属杆处于磁感应强度为B=0.8T,方向与水平方向成60°的匀强磁场中,接通电路后,金属杆ab仍保持静止,求;(g=10m/s2)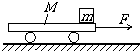 如图所示,质量为M=8kg的小车放在光滑水平面上,在小车右端加一水平恒力F=8N.当小车向右运动的速度达到v0=3m/s,在小车右端轻轻放上一质量m=2kg的小物块,物块与小车间的动摩擦因数μ=0.2,物块始终不离开小车,从小物块放在小车上开始计时.(g取10m/s2)
如图所示,质量为M=8kg的小车放在光滑水平面上,在小车右端加一水平恒力F=8N.当小车向右运动的速度达到v0=3m/s,在小车右端轻轻放上一质量m=2kg的小物块,物块与小车间的动摩擦因数μ=0.2,物块始终不离开小车,从小物块放在小车上开始计时.(g取10m/s2) 静止在光滑水平地面上的平板小车C,质量为mC=3kg,物体A、B的质量为mA=mB=1kg分别以vA=4m/s和vB=2m/s的速度大小,从小车的两端相向地滑到车上.若它们在车上滑动时始终没有相碰,A、B两物体与车的动摩擦因数均为μ=0.2.求:
静止在光滑水平地面上的平板小车C,质量为mC=3kg,物体A、B的质量为mA=mB=1kg分别以vA=4m/s和vB=2m/s的速度大小,从小车的两端相向地滑到车上.若它们在车上滑动时始终没有相碰,A、B两物体与车的动摩擦因数均为μ=0.2.求: