��Ŀ����
4��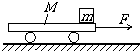 ��ͼ��ʾ������ΪM=8kg��С�����ڹ⻬ˮƽ���ϣ���С���Ҷ˼�һˮƽ����F=8N����С�������˶����ٶȴﵽv0=3m/s����С���Ҷ��������һ����m=2kg��С��飬�����С����Ķ�Ħ��������=0.2�����ʼ�ղ��뿪С������С������С���Ͽ�ʼ��ʱ����gȡ10m/s2��
��ͼ��ʾ������ΪM=8kg��С�����ڹ⻬ˮƽ���ϣ���С���Ҷ˼�һˮƽ����F=8N����С�������˶����ٶȴﵽv0=3m/s����С���Ҷ��������һ����m=2kg��С��飬�����С����Ķ�Ħ��������=0.2�����ʼ�ղ��뿪С������С������С���Ͽ�ʼ��ʱ����gȡ10m/s2����1��t=0ʱ��С�����С�����ٶ�a1��a2
��2��t=2s��С�����С����Ħ������Q
��3��t=7s��С���Ķ���EK��
���� ��1��������С���Ϻ���ţ�ٵڶ�������������С�����ٶȣ�
��2���辭��ʱ��t��С��������ٶ���ȣ����t�������˶�ѧ������ʽ���t=2s��С�����С��������λ�ƣ��ٸ���Q=��mg��x��⣻
��3�����ٺ���F��������һ��������٣�����ţ�ٵڶ����������ʱ�ļ��ٶȣ��ٸ����˶�ѧ������ʽ���7sĩ���ٶȣ����ݶ��ܱ���ʽ��⼴�ɣ�
��� �⣺��1����ţ�ٵڶ����ɿ�֪��
������С���Ϻ��ٶȴ�СΪ${a}_{1}=\frac{��mg}{m}=��g=2m/{s}^{2}$��
С���ļ��ٶȴ�СΪ${a}_{2}=\frac{F-��mg}{M}=0.5m/{s}^{2}$��
��2���辭��ʱ��t��С��������ٶ���ȣ���
a1t=v0+a2t
��ã�t=2s��
����$��x=��{v}_{0}t+\frac{1}{2}{a}_{2}{t}^{2}��-\frac{1}{2}{a}_{1}{t}^{2}$
��С�����С����Ħ������Q=��mg��x=12J
��3����ǰ2sʱ��Ϊt1����5sʱ��Ϊt2�����ٺ���F��������һ��������٣�
���ٶ�a=$\frac{F}{m+M}=\frac{8}{8+2}=0.8m/{s}^{2}$
7sĩ���ٶ�Ϊv2=a1t1+a2t3=8m/s
���Ķ���${E}_{K}=\frac{1}{2}m{{v}_{3}}^{2}=64J$
�𣺣�1��t=0ʱ��С�����С�����ٶȷֱ�Ϊ2m/s2��0.5m/s2��
��2��t=2s��С�����С����Ħ������QΪ12J��
��3��t=7s��С���Ķ���EKΪ64J��
���� ������Ҫ������ţ�ٵڶ����ɡ��˶�ѧ������ʽ��ֱ��Ӧ�ã�֪��С�����С����Ħ����������������Ħ�����������λ�ƣ��Ѷ����У�

 �»����ܶ�Ա��ϵ�д�
�»����ܶ�Ա��ϵ�д� ����ͼ����ּ��������ҵ֣�ݴ�ѧ������ϵ�д�
����ͼ����ּ��������ҵ֣�ݴ�ѧ������ϵ�д� �⻬ˮƽ���ϲ��ŷ��������ֱ�Ϊm1=2kg��m2=1kg������飬t=0ʱ��ͬʱʩ��������������F1=2N��F2=��4-2t��N��������ͼ��ʾ�������������ʱ��Ϊ��������
�⻬ˮƽ���ϲ��ŷ��������ֱ�Ϊm1=2kg��m2=1kg������飬t=0ʱ��ͬʱʩ��������������F1=2N��F2=��4-2t��N��������ͼ��ʾ�������������ʱ��Ϊ��������| A�� | 1s | B�� | 1.5s | C�� | 2s | D�� | 2.5s |
 ��h�ߴ��Գ��ٶ�v0��ֱ�����׳�һ������Ϊm��С����ͼ��ʾ����ȡ�׳���Ϊ���Ƶ㣬���ƿ���������������
��h�ߴ��Գ��ٶ�v0��ֱ�����׳�һ������Ϊm��С����ͼ��ʾ����ȡ�׳���Ϊ���Ƶ㣬���ƿ���������������| A�� | ���׳�������Ļ�е��Ϊmgh | |
| B�� | ����ߵ�����Ļ�е��Ϊ$\frac{1}{2}$mv${\;}_{0}^{2}$ | |
| C�� | ����ߵ�����Ļ�е��Ϊ$\frac{1}{2}$mv${\;}_{0}^{2}$-mgh | |
| D�� | �����ŵ�ʱ�Ļ�е��Ϊmgh+$\frac{1}{2}$mv${\;}_{0}^{2}$ |
| A�� | $\frac{x}{2}$ | B�� | ��$\sqrt{2}$-1��x | C�� | $\frac{x}{4}$ | D�� | $\frac{\sqrt{2}x}{2}$ |
| A�� | ����뾶Խ�����ٶ�ԽС | B�� | ����뾶Խ�����ٶ�Խ�� | ||
| C�� | ����뾶Խ������Խ�� | D�� | ����뾶Խ������ԽС |
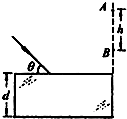 ��ͼ��ʾ�������ƽ�в���ש������Ϊn=$\sqrt{2}$���±�����з���Ĥ��һ����ɫ�������ɦ�=45���б�䵽����ש�����ϣ�����ڲ���ש���Ҳ�����ֱ�����ϳ������������A��B�����h=2.0cm����֪��������еĴ����ٶ�c=3.0��108 m/s����
��ͼ��ʾ�������ƽ�в���ש������Ϊn=$\sqrt{2}$���±�����з���Ĥ��һ����ɫ�������ɦ�=45���б�䵽����ש�����ϣ�����ڲ���ש���Ҳ�����ֱ�����ϳ������������A��B�����h=2.0cm����֪��������еĴ����ٶ�c=3.0��108 m/s����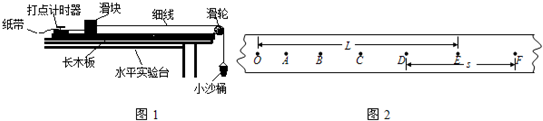
 �����õ��ڲⶨ�������ٶȵ�ʵ����
�����õ��ڲⶨ�������ٶȵ�ʵ���� ��ͼ��ʾ�����dz��õ�һ��ʵ��������������������ʹ���ĵ����뻬��֮���γ����棬ʹ���������ڹ���ϣ������ڹ���ϵ��˶�����Ϊû��Ħ�������ǿ����ô���ֱ����C��D���������Լ�����A��B����֤�����غ㶨�ɣ�ʵ��װ����ͼ��ʾ�����ɵij��Ⱥ��Բ��ƣ������õ�ʵ�鲽�����£�
��ͼ��ʾ�����dz��õ�һ��ʵ��������������������ʹ���ĵ����뻬��֮���γ����棬ʹ���������ڹ���ϣ������ڹ���ϵ��˶�����Ϊû��Ħ�������ǿ����ô���ֱ����C��D���������Լ�����A��B����֤�����غ㶨�ɣ�ʵ��װ����ͼ��ʾ�����ɵij��Ⱥ��Բ��ƣ������õ�ʵ�鲽�����£�