题目内容
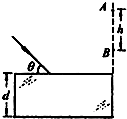
18. 一质量为M,倾角为θ的楔形木块,静置在光滑水平面上,质量为m的物块,置于楔形木块的光滑斜面上.为了保持物块相对斜面静止,可用一水平力F推楔形木块,则( )
一质量为M,倾角为θ的楔形木块,静置在光滑水平面上,质量为m的物块,置于楔形木块的光滑斜面上.为了保持物块相对斜面静止,可用一水平力F推楔形木块,则( )| A. | 楔形木块对物块的支持力为mgcosθ | B. | 楔形木块对物块的支持力为$\frac{mg}{cosθ}$ | ||
| C. | 整体的加速度为gtanθ | D. | F=(M+m)gtanθ |
分析 先对滑块受力分析,然后根据牛顿第二定律并运用合成法求出加速度;再对整体受力分析,根据牛顿第二定律求解出推力F.
解答 解:A、先对m进行研究,受重力mg,斜面支持力N,如图
由于M和m一起向左加速而相对静止,则mg与N合力向右,且合力等于ma.
如图,由数学知识可知
mgtanθ=ma
a=gtanθ
楔形木块对物块的支持力为N=$\frac{mg}{cosθ}$,故A错误,B正确,C正确;
D、再对m和M整体研究
在竖直方向是平衡状态,受重力(M+m)g,受地面支持力FN,且FN=(M+m)g.
水平方向向右匀加速运动,受向右推力F,
根据牛顿第二定律,有
F=(M+m)a=(M+m)gtanθ,故D正确;
故选:BCD.
点评 本题关键先对滑块受力分析后运用牛顿第二定律求出加速度,再对整体受力分析后运用牛顿第二定律求解推力F.

练习册系列答案
相关题目
8. 平抛运动可以分解为水平和竖直方向的两个直线运动,在同一坐标系中作出这两个分运动的v-t图线,如图所示.若平抛运动的时间等于2t1,则下列说法正确的是( )
平抛运动可以分解为水平和竖直方向的两个直线运动,在同一坐标系中作出这两个分运动的v-t图线,如图所示.若平抛运动的时间等于2t1,则下列说法正确的是( )
 平抛运动可以分解为水平和竖直方向的两个直线运动,在同一坐标系中作出这两个分运动的v-t图线,如图所示.若平抛运动的时间等于2t1,则下列说法正确的是( )
平抛运动可以分解为水平和竖直方向的两个直线运动,在同一坐标系中作出这两个分运动的v-t图线,如图所示.若平抛运动的时间等于2t1,则下列说法正确的是( )| A. | t1时刻的速度方向与初速度方向夹角为45° | |
| B. | 2t1时刻的动能是初动能的4倍 | |
| C. | 0-t1时间内重力的功率与t1-2t1时间内重力的功率之比为1:2 | |
| D. | 图线b的斜率为一常量,与坐标轴标度的选取无关 |
3.关于力对物体的做功情况,下列说法正确的是( )
| A. | 物体做自由落体运动时,重力对物体一定做功 | |
| B. | 行星绕太阳在圆轨道上运行时,引力对物体不做功 | |
| C. | 沿斜坡向上加速行驶的汽车,牵引力一定做功 | |
| D. | 细绳的一端固定,另一端拴一小球,使小球在竖直平面的拉力要做功 |
10. 光滑水平面上并排放置质量分别为m1=2kg、m2=1kg的两物块,t=0时刻同时施加两个力,其中F1=2N、F2=(4-2t)N,方向如图所示,则两物块分离的时刻为( )
光滑水平面上并排放置质量分别为m1=2kg、m2=1kg的两物块,t=0时刻同时施加两个力,其中F1=2N、F2=(4-2t)N,方向如图所示,则两物块分离的时刻为( )
 光滑水平面上并排放置质量分别为m1=2kg、m2=1kg的两物块,t=0时刻同时施加两个力,其中F1=2N、F2=(4-2t)N,方向如图所示,则两物块分离的时刻为( )
光滑水平面上并排放置质量分别为m1=2kg、m2=1kg的两物块,t=0时刻同时施加两个力,其中F1=2N、F2=(4-2t)N,方向如图所示,则两物块分离的时刻为( )| A. | 1s | B. | 1.5s | C. | 2s | D. | 2.5s |
13.一个物体以角速度ω做匀速圆周运动时,下列说法中正确的是( )
| A. | 轨道半径越大线速度越小 | B. | 轨道半径越大线速度越大 | ||
| C. | 轨道半径越大周期越大 | D. | 轨道半径越大周期越小 |
 如图所示,真空中平行玻璃砖折射率为n=$\sqrt{2}$,下表面镀有反射膜,一束单色光与界面成θ=45°角斜射到玻璃砖表面上,最后在玻璃砖的右侧面竖直光屏上出现了两个光点A和B,相距h=2.0cm.已知光在真空中的传播速度c=3.0×108 m/s.求:
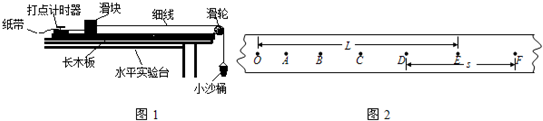
如图所示,真空中平行玻璃砖折射率为n=$\sqrt{2}$,下表面镀有反射膜,一束单色光与界面成θ=45°角斜射到玻璃砖表面上,最后在玻璃砖的右侧面竖直光屏上出现了两个光点A和B,相距h=2.0cm.已知光在真空中的传播速度c=3.0×108 m/s.求: 研究匀变速直线运动的实验中打出的纸带如图所示.图中O,A,B,C,D,E均为记数点,相邻两记数点之间均包含5个自然打点间隔.测量记数点间距时,用刻度尺的零刻线与纸带打出起始点O对齐,由A至E各点对应的刻度值分别为7.0,11.0,17.0,25.0和35.0(单位为cm).根据纸带求出
研究匀变速直线运动的实验中打出的纸带如图所示.图中O,A,B,C,D,E均为记数点,相邻两记数点之间均包含5个自然打点间隔.测量记数点间距时,用刻度尺的零刻线与纸带打出起始点O对齐,由A至E各点对应的刻度值分别为7.0,11.0,17.0,25.0和35.0(单位为cm).根据纸带求出