题目内容
17.201年11月3日,“神州八号”飞船与“天宫一号”目标飞行器成功实施了首次交会对接.任务完成后“天宫一号”经变轨升到更高的轨道,等待与“神州九号”交会对接.变轨前和变轨完成后“天宫一号”的运行轨道均可视为圆轨道,对应的轨道半径分别为R1、R2,线速度大小分别为v1、v2,则$\frac{{V}_{1}}{{V}_{2}}$ 等于( )| A. | $\frac{{{R}_{2}}^{2}}{{{R}_{1}}^{2}}$ | B. | $\sqrt{\frac{{{R}_{1}}^{3}}{{{R}_{2}}^{3}}}$ | C. | $\frac{{R}_{2}}{{R}_{1}}$ | D. | $\sqrt{\frac{{R}_{2}}{{R}_{1}}}$ |
分析 天宫一号绕地球做匀速圆周运动,靠万有引力提供向心力,根据万有引力定律和牛顿第二定律比较线速度的大小关系.
解答 解:“神舟八号”飞船与“天宫一号”绕地球做匀速圆周运动,靠万有引力提供向心力:
$\frac{GMm}{{R}^{2}}$=m$\frac{{v}^{2}}{R}$
得:v=$\sqrt{\frac{GM}{R}}$,
所以$\frac{{v}_{1}}{{v}_{2}}$=$\sqrt{\frac{{R}_{2}}{{R}_{1}}}$.故D正确、ABC错误.
故选:D
点评 本题的关键根据万有引力提供向心力$\frac{GMm}{{R}^{2}}$=m$\frac{{v}^{2}}{R}$,解出线速度与轨道半径的关系.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
8. 平抛运动可以分解为水平和竖直方向的两个直线运动,在同一坐标系中作出这两个分运动的v-t图线,如图所示.若平抛运动的时间等于2t1,则下列说法正确的是( )
平抛运动可以分解为水平和竖直方向的两个直线运动,在同一坐标系中作出这两个分运动的v-t图线,如图所示.若平抛运动的时间等于2t1,则下列说法正确的是( )
 平抛运动可以分解为水平和竖直方向的两个直线运动,在同一坐标系中作出这两个分运动的v-t图线,如图所示.若平抛运动的时间等于2t1,则下列说法正确的是( )
平抛运动可以分解为水平和竖直方向的两个直线运动,在同一坐标系中作出这两个分运动的v-t图线,如图所示.若平抛运动的时间等于2t1,则下列说法正确的是( )| A. | t1时刻的速度方向与初速度方向夹角为45° | |
| B. | 2t1时刻的动能是初动能的4倍 | |
| C. | 0-t1时间内重力的功率与t1-2t1时间内重力的功率之比为1:2 | |
| D. | 图线b的斜率为一常量,与坐标轴标度的选取无关 |
12.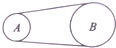 如图所示,在皮带传动装置中,主动轮A和从动轮B半径之比为RA:RB=1:3,皮带与轮之间无相对滑动,关于两轮边缘上点的四个物理量大小之间的下列关系,正确的是( )
如图所示,在皮带传动装置中,主动轮A和从动轮B半径之比为RA:RB=1:3,皮带与轮之间无相对滑动,关于两轮边缘上点的四个物理量大小之间的下列关系,正确的是( )
 如图所示,在皮带传动装置中,主动轮A和从动轮B半径之比为RA:RB=1:3,皮带与轮之间无相对滑动,关于两轮边缘上点的四个物理量大小之间的下列关系,正确的是( )
如图所示,在皮带传动装置中,主动轮A和从动轮B半径之比为RA:RB=1:3,皮带与轮之间无相对滑动,关于两轮边缘上点的四个物理量大小之间的下列关系,正确的是( )| A. | vA:vB=1:3 | B. | TA:TB=3:1 | C. | ωA:ωB=3:1 | D. | aA:aB=1:3 |

 如图所示,真空中平行玻璃砖折射率为n=$\sqrt{2}$,下表面镀有反射膜,一束单色光与界面成θ=45°角斜射到玻璃砖表面上,最后在玻璃砖的右侧面竖直光屏上出现了两个光点A和B,相距h=2.0cm.已知光在真空中的传播速度c=3.0×108 m/s.求:
如图所示,真空中平行玻璃砖折射率为n=$\sqrt{2}$,下表面镀有反射膜,一束单色光与界面成θ=45°角斜射到玻璃砖表面上,最后在玻璃砖的右侧面竖直光屏上出现了两个光点A和B,相距h=2.0cm.已知光在真空中的传播速度c=3.0×108 m/s.求: 研究匀变速直线运动的实验中打出的纸带如图所示.图中O,A,B,C,D,E均为记数点,相邻两记数点之间均包含5个自然打点间隔.测量记数点间距时,用刻度尺的零刻线与纸带打出起始点O对齐,由A至E各点对应的刻度值分别为7.0,11.0,17.0,25.0和35.0(单位为cm).根据纸带求出
研究匀变速直线运动的实验中打出的纸带如图所示.图中O,A,B,C,D,E均为记数点,相邻两记数点之间均包含5个自然打点间隔.测量记数点间距时,用刻度尺的零刻线与纸带打出起始点O对齐,由A至E各点对应的刻度值分别为7.0,11.0,17.0,25.0和35.0(单位为cm).根据纸带求出