题目内容
【题目】如图所示,无限长金属导轨EF、PQ固定在倾角为θ=37°的光滑绝缘斜面上,轨道间距L=1 m,底部接入一阻值为R=0.06Ω的定值电阻,上端开口。垂直斜面向上的匀强磁场的磁感应强度Bo=2T。一质量为m=2kg的金属棒ab与导轨接触良好,ab与导轨间动摩擦因数μ=0.5,ab连入导轨间的电阻r=0.04Ω,电路中其余电阻不计。现用一质量为M=6kg的物体通过一不可伸长的轻质细绳绕过光滑的定滑轮与ab相连。由静止释放M,当M下落高度h=2.0 m时,ab开始匀速运动(运动中ab始终垂直导轨,并接触良好)。不计空气阻力,sin37°=0.6,cos37°=0.8,取g=10m/s2。求:
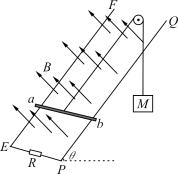
(1)ab棒沿斜面向上运动的最大速度vm;
(2)ab棒从开始运动到匀速运动的这段时间内电阻R上产生的焦耳热QR;
(3)若将重物下降h时的时刻记作t=0,从此时刻起,磁感应强度发生变化,使金属杆中恰好不产生感应电流,则B与t应满足怎样的关系式?
【答案】(1)1m/s(2)45.6J(3)![]()
【解析】
试题分析: (1)由题意知,由静止释放M后,ab棒在绳拉力T、重力mg、安培力F和轨道支持力N及摩擦力f共同作用下做沿轨道向上做加速度逐渐减小的加速运动直至匀速运动,当达到最大速度时有:
T-mgsinθ-F-f=0…①
N-mgcosθ=0…②
又 T=Mg…③
f=μN…④
安培力为 F=BIL…⑤
感应电流为:![]() …⑥
…⑥
联解①②③④⑤⑥并代入数据得:vm=1m/s…⑦
(2)由能量守恒定律知,系统的总能量守恒,即系统减少的重力势能等于系统增加的动能、焦耳热及摩擦而转化的内能之和,有:
Mgh-mghsinθ=μmghcosθ+![]() (m+M)vm2+Q…⑧
(m+M)vm2+Q…⑧
而电阻R上产生的焦耳热 ![]() …⑨
…⑨
联解⑦⑧⑨⑩并代入数据得:QR=45.6J…
(3)回路中总磁通量不变,ab不产生感应电流,沿导轨匀加速上滑,对M和ab系统有:![]()
解得:a=5m/s2
又![]()
解得![]()

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案