题目内容
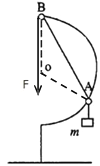
【题目】(2015·上海)如图,在场强大小为E、水平向右的匀强电场中,一轻杆可绕固定转轴O在竖直平面内自由转动。杆的两端分别固定两电荷量均为q的小球A、B;A带正电,B带负电;A、B两球到转轴O的距离分别为2l、l , 所受重力大小均为电场力大小的![]() 倍,开始时杆与电场夹角为
倍,开始时杆与电场夹角为![]() (90°≤
(90°≤![]() ≤180°)。将杆从初始位置由静止释放,以O点为重力势能和电势能零点。求:
≤180°)。将杆从初始位置由静止释放,以O点为重力势能和电势能零点。求: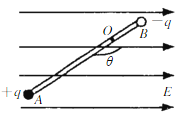
(1)初始状态的电势能We
(2)杆在平衡位置时与电场间的夹角![]()
(3)杆在电势能为零处的角速度![]()
【答案】
(1)
-3qElcos![]() .
.
(2)
30°
(3)
当![]() <150°,
<150°, ![]() =
=![]() , 当
, 当![]() >150°,
>150°, ![]() =
=![]() 或
或![]()
【解析】初态:We=qV++(-q)V=q(V+-V-)=-3qElcos![]() .
.
(2)平衡位置如图,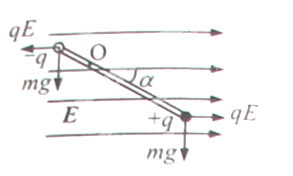
设小球的质量为m,合力矩为
3qELsin![]() -mglcos
-mglcos![]() =0
=0
由此得tan![]() =
=![]()
![]() =30°
=30°
(3)电势能为零时,杆处于竖直位置,当初始时OA与电场间夹角θ=150°时,A恰好能到达O正上方,在此位置杆的角速度为0
当![]() <150°时,A位于O正下方处电势能为零。
<150°时,A位于O正下方处电势能为零。
初态:We=—3qElcos![]() , Ep=mglsin
, Ep=mglsin![]()
末态: We'=0, Ep'=-mgl
能量守恒:-3qELcos![]() -mglsin
-mglsin![]() =
=![]() ml2w2-mgl
ml2w2-mgl![]()
![]()
当θ≥150°时,电势能为0有两处,即A位于O正下方或正上方处
当A位于O正下方时,![]()
解得 =![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目