题目内容
【题目】如图所示,充电后的平行板电容器水平放置,电容为C,极板间距离为d,上极板正中有一小孔,质量为m、电荷量为+q的小球从小孔正上方高h处由静止开始下落,穿过小孔到达下极板处速度恰为零(空气阻力忽略不计,极板间电场可视为匀强电场,重力加速度为g),求:
(1)小球到达小孔处的速度;
(2)极板间电场强度大小和电容器所带电荷量;
(3)小球从开始下落运动到下极板处的时间.
【答案】
(1)
解:小球到达小孔前是自由落体运动,根据速度位移关系公式,有:
v2=2gh
解得:
v= ![]() …①
…①
(2)
解:对从释放到到达下极板处过程运用动能定理列式,有:
mg(h+d)﹣qEd=0
解得:
E= ![]() …②
…②
电容器两极板间的电压为:
U=Ed= ![]() ,
,
电容器的带电量为:
Q=CU= ![]()
(3)
解:加速过程:
mgt1=mv…③
减速过程,有:
(mg﹣qE)t2=0﹣mv…④
t=t1+t2…⑤
联立①②③④⑤解得:
t= ![]()
【解析】(1)小球到达小孔前是自由落体运动,根据速度位移关系公式列式求解即可;(2)对从释放到到达下极板处过程运用动能定理列式求解电场强度,然后根据Q=CU求解电容器的带电量;(3)对加速过程和减速过程分别运用动量定理列式求解时间,然后求和即可.

 阅读快车系列答案
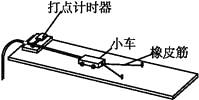
阅读快车系列答案【题目】某同学利用图甲所示装置探究力对物体做的功与物体速度变化的关系,得到了下表的数据:
实验次数 | 1 | 2 | 3 | 4 | 5 |
橡皮筋条数 | 1 | 3 | 4 | 5 | 7 |
小车速度v/(m·s-1) | 0.71 | 1.23 | 1.42 | 1.58 | 1.71 |
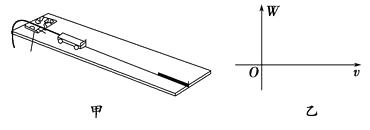
(注:每条橡皮筋拉长的长度都一样)
(1)由表可得出定性结论:.
(2)设一条橡皮筋拉长到固定长度所做功为W0 , 大致画出橡皮筋所做的功W与小车速度v的图象.(画在图乙中)
(3)根据以上的W-v图象对W与v的关系作出初步判断: .
(4)根据数据完成下表的空白部分:
实验次数 | 1 | 2 | 3 | 4 | 5 |
橡皮筋做功 | W0 | ||||
v2/(m2·s-2) | |||||
W与v的关系 | |||||