题目内容
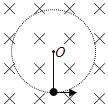
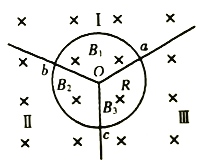
【题目】如图所示，由Oa、Ob、Oc三个铝制薄板互成120°角均匀分开的I、Ⅱ、Ⅲ三个匀强磁场区域，其磁感应强度分别用B1、B2、B3表示。现有带电粒子自a点垂直Oa板沿逆时针方向射入磁场中，带电粒子完成一周运动，假设带电粒子穿过铝质薄板过程中电荷量不变，在三个磁场区域中的运动时间之比为1：3：5，轨迹恰好是一个以O为圆心的圆，不计粒子重力，则
X
A. 磁感应强度B1：B2：B3=1：3：5
B. 磁感应强度B1：B2：B3=5：3：1
C. 其在b、c处穿越铝板所损失的动能之比为25：2
D. 其在b、c处穿越铝板所损失的动能之比为27：5
【答案】C
【解析】试题分析：利用洛伦兹力提供向心力求出半径公式，结合粒子在三个区域中运动的半径相同，粒子在三个区域中运动的时间之比为1：3：5，结合粒子转过的圆心角，再利用比例性质，联立即可求出粒子在b、c处穿越铝板所损失的动能之比．
带电粒子在磁场中运动的时间为
，在各个区域的角度均为
，根据洛伦兹力提供向心力可得
，粒子在磁场中的运动的周期
，所以
，故
，又因为m、q均为定值，则三个区域的磁场应强度之比为：
，AB错误；三个区域的磁场半径相同，为
，又因为动能：
，联立可得
，因为q、m和r均相同，故三个区域中运动的动能之比为
，设比例中的每一份为k，在b处穿越铝板所损失的动能为
，在c处穿越铝板所损失的动能为
，所以可得其在b、c处穿越铝板所损失的动能之比
，C正确D错误．
练习册系列答案
名校课堂系列答案
相关题目
