题目内容
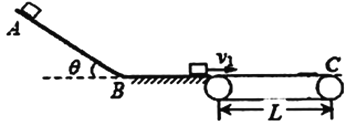
【题目】如图所示,两根金属平行导轨MN和PQ放在水平面上,左端向上弯曲且光滑,导轨间距为L,电阻不计。水平段导轨所处空间有匀强磁场,磁感应强度大小为B,方向竖直向上,磁场区域足够大。两个电阻均为R、质量均为m的金属棒a和b垂直导轨放置在其上。现将金属棒a从弯曲导轨上、距水平轨道高度为h处由静止释放,使其沿导轨运动并进入磁场。设两金属棒运动过程中始终未相碰,与导轨垂直且接触良好。
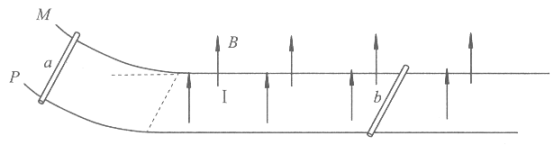
(1)对全过程进行研究:
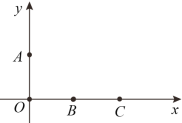
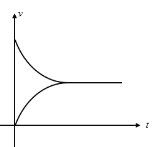
①在同一坐标系中画出两个金属棒的速度随时间变化图像(从a进入磁场开始计时);
②求金属棒b的最终速度;
③求回路中产生的总焦耳热;
(2)对运动过程中的某一状态进行
a进入磁场后某时刻,a的速度为v1,b的速度为v2,此时,a克服安培力做功的功率为P1,安培力对b做功的功率为P2,回路中的焦耳热功率为P3,请写出P1、P2、P3三者的关系,并写出证明过程。
【答案】(1)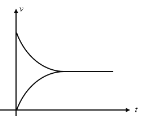
![]() ,
,![]() mgh,(2)P1=P2+P3
mgh,(2)P1=P2+P3
【解析】
(1)①a进入磁场后,回路中产生感应电流,a、b都受安培力作用,a做减速运动,b做加速运动,两者的加速度都逐渐减小,经一段时间,a、b速度达到相同,之后回路的磁通量不发生变化,感应电流为零,安培力为零,两者做匀速运动
在同一坐标系中画出两个金属棒的速度随时间变化图像(从a进入磁场开始计时);如图所示
②a下滑h的过程中机械能守恒:mgh=![]()
在水平轨道上运动的过程中a、b组成的系统所受合外力为零,由动量守恒得:
![]()
由上式解得最终速度
v=![]()
③由能量守恒定律得,回路中产生的总焦耳热
![]()
(2)两个导体棒切割磁感线产生的感应电动势
![]()
由闭合电路欧姆定律得:
![]()
两个棒受到的安培力
![]()
a克服安培力做功的功率为P1
![]()
安培力对b做功的功率为P2
![]()
回路中的焦耳热功率为P3
![]()
所以P1、P2、P3三者的关系为
P1=P2+P3