题目内容
【题目】设地球可看作半径![]() 的球体,一颗人造地球卫星在地面上空
的球体,一颗人造地球卫星在地面上空![]() 的圆形轨道上以
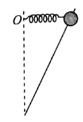
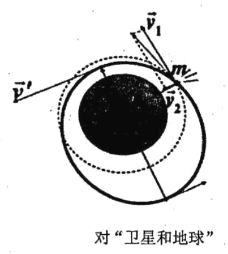
的圆形轨道上以![]() 的速度绕地球运动。今在卫星外侧,点燃一个小火箭,给卫星附加一个指向地心的分速度
的速度绕地球运动。今在卫星外侧,点燃一个小火箭,给卫星附加一个指向地心的分速度![]() ,求此后卫星的椭圆轨道的近地点和远地点离地面多少?
,求此后卫星的椭圆轨道的近地点和远地点离地面多少?
【答案】近地点高度![]() ,远地点高度
,远地点高度![]()
【解析】
设火箭点燃时,卫星![]() 对地形的位失为
对地形的位失为![]() ,速度为
,速度为![]() ,使卫星转为椭圆轨道
,使卫星转为椭圆轨道
因为对o点的![]() 所以对o点角动量守恒。在近地点时,位矢为
所以对o点角动量守恒。在近地点时,位矢为![]() ,速度位
,速度位![]() ,则有
,则有
![]()
![]() (
(![]() )=
)=![]()
![]()
![]()
![]()
![]() (
(![]() )=
)=![]()
![]()
![]()

或者表述为:火箭点燃时卫星转为椭圆轨道,近(远)地点是卫星速度垂直于地心到卫星的直线,所以根据对o点角动量守恒有:
![]() (1)
(1)
因为做椭圆运动时,只有万有引力做功,机械能守恒,有:
![]()
为了免去G、M的计算,通常利用卫星做圆周运动的向心力(既万有引力)来简化上式:
![]()
代入机械能守恒式得:
![]() (2)
(2)
(2)联立,将(1)中的v′代入(2)中,可得:
![]()
![]()
解出:
![]()
近地点高度:
![]()
同理:
![]()
远地点高度:
![]()

练习册系列答案
相关题目