题目内容

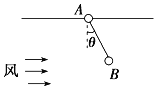
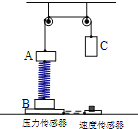
【题目】如图，一根长为L=1.25m的轻绳一端固定在O’点，另一端系一质量m=1kg的小球。将轻绳拉至水平并将小球由位置A静止释放，小球运动到最低点O时，轻绳刚好被拉断。O′点下方有一以O点为圆心，半径R=5m的圆弧状的曲面，己知重力加速度为g=10m/s2，求：

（1）轻绳所能承受的最大拉力Fm的大小；

（2）小球从绳子断裂到落至曲面上的时间和到达曲面时的动能。

【答案】（1）30N；（2）62.5J

【解析】

（1）物体从A运动到O点，由机械能守恒定律：mgL=
得：v0=
在O点，由牛顿第二定律：
得：Fm=3mg=30N
（2）设从绳子断裂到小球到达曲面经历的时间为t，
水平位移：x=v0t
竖直位移：y=
由勾股定理：x2+y2=R2
解得t=1s
竖直速度：vy=gt=10m/s
可得小球的动能：=62.5J

练习册系列答案
相关题目

【题目】如图所示，虚线MN左侧有一场强为E1＝E的匀强电场，在两条平行的虚线MN和PQ之间存在着宽为L、电场强度为E2＝2E的匀强电场，在虚线PQ右侧距PQ为L处有一与电场E2平行的屏．现将一电子(电荷量为e，质量为m，重力不计)无初速度地放入电场E1中的A点，最后电子打在右侧的屏上，A点到MN的距离为，AO连线与屏垂直，垂足为O，求：

(1) 电子从释放到打到屏上所用的时间；

(2) 电子离开偏转电场时偏转角的正切值tanθ；

(3) 电子打到屏上的点P′到点O的距离.

【题目】如图所示，质量M＝2 kg的平板小车后端放有质量m＝3 kg的铁块，它和车之间的动摩擦因数μ＝0.5，开始时车和铁块一起以v0＝3 m/s的速度向右在光滑水平地面上向右运动，并与竖直墙壁发生碰撞．设碰撞时间极短且碰撞后平板车速度大小保持不变，但方向与原来相反，平板车足够长，使得铁块总不能和墙相碰．(g取10 m/s2)求：

(1)铁块在车上滑行的总路程；

(2)车和墙第一次相碰以后所走的总路程．

【题目】如图所示，a为xOy坐标系x负半轴上的一点，空间有平行于xOy坐标平面的匀强电场，一个质量为m、电荷量为q的带正电粒子以初速度v0从a点沿与x轴正半轴成θ角斜向右上射入电场，粒子只在电场力作用下运动，经过y正半轴上的b点(图中未标出)，则下列说法正确的是

A. 若粒子在b点速度方向沿x轴正方向，则电场方向可能平行于x轴

B. 若粒子运动过程中在b点速度最小，则b点为粒子运动轨迹上电势最低点

C. 若粒子在b点速度大小也为v0，则a、b两点电势相等

D. 若粒子在b点的速度为零，则电场方向一定与v0方向相反

【题目】如图，间距L=0.5m的平行金属导轨固定在水平面（纸面）上，导轨间接一电阻，质量m=0.1kg的金属杆置于导轨上。t0=0时，金属杆在水平向右的恒定拉力作用下由静止开始运动。t1=5s时，金属杆以速度v=4m/s进入磁感应强度B0=0.8T、方向竖直向下的匀强磁场区域，且在磁场中恰好能保持匀速运动。在t2=8s时撤去拉力，同时磁场的磁感应强度开始逐渐减小，此后金属杆做匀减速运动到t3=10s时停止，此时磁感应强度仍未减小到零。金属杆与导轨的电阻不计，两者始终保持垂直且接触良好，两者之间的动摩擦因数μ=0.2。取g=10m/s2。求：

（1）电阻的阻值；

（2）t3=10s时磁场的磁感应强度大小。

【题目】2019年1月3日，“嫦娥四号”探测器完成了人类历史上的首次月背软着陆．“嫦娥四号”的核电池利用放射性同位素Pu衰变供电；静止的Pu衰变为铀核和X粒子，放出频率为ν的γ光子．已知：Pu、和X粒子的质量分别为mPu、mU和mX，普朗克常数为h，光速为c．则下列说法正确的是

A. X粒子是He

B. 的比结合能比Pu的大

C. 释放出的γ光子能量为(mPu- mU)c2

D. 放射性同位素Pu的半衰期随温度降低而变大

【题目】如图，a、b、c、…、k为连续的弹性介质中间隔相等的若干质点，e点为波源，t＝0时刻从平衡位置开始向上做简谐运动，振幅为3 cm，周期为0.2 s．在波的传播方向上，后一质点比前一质点迟0.05 s开始振动．t＝0.25 s时，x轴上距e点2.0 m的某质点第一次到达最高点，则

A. 该机械波在弹性介质中的传播速度为8m/s

B. 该机械波的波长为2 m

C. 图中相邻质点间距离为0.5 m

D. 当b点在平衡位置上方3cm处时，f点也在平衡位置上方3cm处

【题目】如图所示，水平细杆上套一球A，球A与球B间用一轻绳相连，质量分别为mA和mB，由于B球受到水平风力作用，球A与球B一起向右匀速运动。已知细绳与竖直方向的夹角为θ，则下列说法中正确的是（　　）

A.球A与水平细杆间的动摩擦因数为

B.球B受到的风力F为

C.风力增大时，若A、B仍匀速运动，轻质绳对球B的拉力保持不变

D.杆对球A的支持力随着风力的增加保持不变

【题目】某同学利用如图装置来研究机械能守恒问题，设计了如下实验．A、B是质量均为m的小物块，C是质量为M的重物，A、B间由轻弹簧相连，A、C间由轻绳相连．在物块B下放置一压力传感器，重物C下放置一速度传感器，压力传感器与速度传感器相连．当压力传感器示数为零时，就触发速度传感器测定此时重物C的速度．整个实验中弹簧均处于弹性限度内，重力加速度为g．实验操作如下：

(1)开始时，系统在外力作用下保持静止，细绳拉直但张力为零．现释放C，使其向下运动，当压力传感器示数为零时，触发速度传感器测出C的速度为v．

(2)在实验中保持A，B质量不变，改变C的质量M，多次重复第(1)步．

①该实验中，M和m大小关系必需满足M______m　（选填“小于”、“等于”或“大于”）

②为便于研究速度v与质量M的关系，每次测重物的速度时，其已下降的高度应______（选填“相同”或“不同”）

③根据所测数据，为得到线性关系图线，应作出______（选填“v2-M”、“v2-”或“v2-”）图线．

④根据③问的图线知，图线在纵轴上截距为b，则弹簧的劲度系数为______（用题给的已知量表示）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网