题目内容
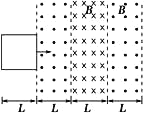
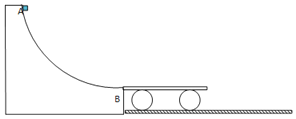
【题目】如图所示,质量M=2 kg的平板小车后端放有质量m=3 kg的铁块,它和车之间的动摩擦因数μ=0.5,开始时车和铁块一起以v0=3 m/s的速度向右在光滑水平地面上向右运动,并与竖直墙壁发生碰撞.设碰撞时间极短且碰撞后平板车速度大小保持不变,但方向与原来相反,平板车足够长,使得铁块总不能和墙相碰.(g取10 m/s2)求:
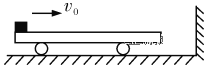
(1)铁块在车上滑行的总路程;
(2)车和墙第一次相碰以后所走的总路程.
【答案】(1)1.5 m(2)1.25 m
【解析】
(1)由于m>M,小车不论与墙相撞多少次,系统的总动量总是向右,但每撞一次总动量减少一次,直到减为零,最后小车停在墙下,系统的总动能全部用于铁块在车上滑行时克服摩擦力做功.
μmgs=![]() (m+M)v02
(m+M)v02
![]()
(2)小车第一次与墙相撞后向左所走路程为s1,由动能定理得-μmgs1=0-![]() Mv02
Mv02
![]()
接着小车和铁块以共同速度v1与墙第二次相碰,由动量守恒:
mv0-Mv0=(m+M)v1
![]()
第二次相撞后平板车向左走的路程为![]() ,s2=
,s2=![]() s1以后每次相碰反弹向左行的路程均以
s1以后每次相碰反弹向左行的路程均以![]() 比例减少,小车所走的路程为一个无穷等比数列之和.
比例减少,小车所走的路程为一个无穷等比数列之和.
公比q=![]() ,s=2s1(1+q+q2+q3+……)=
,s=2s1(1+q+q2+q3+……)=![]() =1.25 m
=1.25 m

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目