题目内容
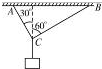如图所示，用绳AC和BC吊起一重物，绳与竖直方向夹角分别为30°和60°，AC绳能承受的最大拉力为150N，而BC绳能承受的最大拉力为100N，求物体最大重力不能超过多少？分析：对结点受力分析后，应用平衡条件求解出AC绳和BC绳上的拉力关系，根据两绳所能承受的最大拉力判断谁先断，按照最小的求解即可．
解答：解析：以重物为研究对象．受力如右图所示，
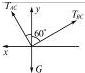
由平衡条件得：
TACsin30°-TBCsin60°=0①
TACcos30°+TBCcos60°-G=0②
由式①可知TAC=
TBC
当TBC=100N时，TAC=173N，AC将断．
而当TAC=150N时，TBC=86.6N＜100N
将TAC=150N，TBC=86.6N代入式②解得G=173.2N
所以重物的最大重力不能超过173.2 N．
答：物体最大重力不能超过173.2N
由平衡条件得：
TACsin30°-TBCsin60°=0①
TACcos30°+TBCcos60°-G=0②
由式①可知TAC=
| 3 |
当TBC=100N时，TAC=173N，AC将断．
而当TAC=150N时，TBC=86.6N＜100N
将TAC=150N，TBC=86.6N代入式②解得G=173.2N
所以重物的最大重力不能超过173.2 N．
答：物体最大重力不能超过173.2N
点评：本题为平衡条件的应用，受力分析后根据临界条件进行判断即可．
练习册系列答案
相关题目
．如图所示，用绳AC和BC吊起一个物体，它们与水平方向的夹角分别为37°和53°，若物体的重力为100N，则两条绳所承受的拉力分别为多大？若AC绳能承受的最大拉力为200N，BC绳能承受的最大拉力为250N在增加重物的重力过程中，哪条绳先断？（sin37°=0.6，cos37°=0.8）
如图所示，用绳AC和BC吊起一个物体，绳AC与竖直方向的夹角为60°，能承受的最大拉力为100N，绳BC与竖直方向的夹角为30°能承受的最大拉力为150N．欲使两绳都不断，物体的重力不应超过多少？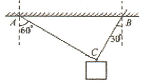
如图所示，用绳AC和BC吊起一个物体，绳AC与竖直方向的夹角为60°，能承受最大拉力为100N；绳BC与竖直方向的夹角为30°，能承受的最大拉力为150N．欲使两绳都不断，物体的重力不应超过（ ）
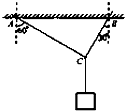如图所示，用绳AC和BC吊起一个物体，绳AC与竖直方向的夹角为60°，绳BC与竖直方向的夹角为30°，两绳能承受的最大拉力均为100N，g=10m/s2，求：