题目内容
19.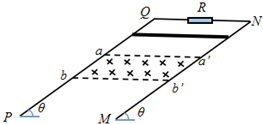 如图所示,两根平行的光滑的金属导轨PQ和MN相距L,它们与水平方向的夹角为θ,导轨的上方跟电阻R相连,在导轨的下端有一宽度为d(即ab=d)磁感应强度为B的有界匀强磁场,磁场的边界aa′和bb′垂直于导轨,磁场的方向与导轨平面垂直,质量为m的电阻不计的导体棒从某位置静止释放,恰好能匀速地通过磁场区域.若当地的重力加速度为g,求:
如图所示,两根平行的光滑的金属导轨PQ和MN相距L,它们与水平方向的夹角为θ,导轨的上方跟电阻R相连,在导轨的下端有一宽度为d(即ab=d)磁感应强度为B的有界匀强磁场,磁场的边界aa′和bb′垂直于导轨,磁场的方向与导轨平面垂直,质量为m的电阻不计的导体棒从某位置静止释放,恰好能匀速地通过磁场区域.若当地的重力加速度为g,求:(1)开始释放时,棒与aa′之间的距离x;
(2)棒通过磁场的过程中所生的热.
分析 (1)根据动能定理,结合受力平衡条件,及切割感应电动势与闭合电路欧姆定律,即可求解;
(2)根据能量守恒:重力势能转化为热量,即可求得.
解答 解:(1)设导体进入磁场时的速度为v0,根据动能定理得:
mgxsinθ=$\frac{1}{2}m{v}_{0}^{2}$
由棒匀速通过磁场可知合外力为零,则棒在磁场所受的安培力为F安:
F安=mgsinθ=BIL
闭合电路欧姆定律,I=$\frac{E}{R}$
切割感应电动势,E=BLv0
联立得:x=$\frac{{m}^{2}{R}^{2}gsinθ}{2{B}^{4}{L}^{4}}$
(2)根据能量守恒定律:动能不变,重力势能全部转化为热量Q
Q=mgdsinθ
答:(1)开始释放时,棒与aa′之间的距离$\frac{{m}^{2}{R}^{2}gsinθ}{2{B}^{4}{L}^{4}}$;
(2)棒通过磁场的过程中所生的热量mgdsinθ.
点评 考查动能定理、能量守恒定律内容,掌握法拉第电磁感应定律与闭合电路欧姆定律的应用,理解平衡条件的运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.下列说法中正确的是( )
| A. | 功是矢量,正、负表示方向 | |
| B. | 功是标量,正、负表示外力对物体做功还是物体克服外力做功 | |
| C. | 力对物体做正功还是做负功,取决于力和位移的方向关系 | |
| D. | 力做功总是在某过程中完成的,所以功是一个过程量 |
7.将卫星发射至近地圆轨道1,然后再次点火,将卫星送入同步轨道3.轨道1、2相切于Q点,2、3相切于P点,则当卫星分别在1、2、3轨道上正常运行时(如图所示),以下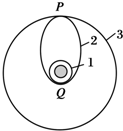 说法正确的是( )
说法正确的是( )
 说法正确的是( )
说法正确的是( )| A. | 卫星在轨道3上的速率大于轨道1上的速率 | |
| B. | 卫星在轨道3上的角速度小于在轨道1上的角速度 | |
| C. | 卫星在轨道1上经过Q点时的加速度大于它在轨道2上经过Q点时的加速度 | |
| D. | 卫星在轨道2上经过P点的加速度等于它在轨道3上经过P点时的加速度 |
14.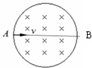 如图所示,在圆形区域内有方向垂直向里的匀强磁场.有一束速率各不相同的质子沿直径AB射入磁场,这些质子在磁场中( )
如图所示,在圆形区域内有方向垂直向里的匀强磁场.有一束速率各不相同的质子沿直径AB射入磁场,这些质子在磁场中( )
 如图所示,在圆形区域内有方向垂直向里的匀强磁场.有一束速率各不相同的质子沿直径AB射入磁场,这些质子在磁场中( )
如图所示,在圆形区域内有方向垂直向里的匀强磁场.有一束速率各不相同的质子沿直径AB射入磁场,这些质子在磁场中( )| A. | 所有质子在磁场中的运动时间相同 | |
| B. | 所有质子均从AB下方离开磁场 | |
| C. | 速度越大的,磁场中运动的时间越长 | |
| D. | 速度越大的,速度的偏转角越小 |
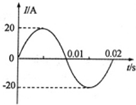 一个正弦规律变化的交变电流的图象如图所示,根据图象计算:
一个正弦规律变化的交变电流的图象如图所示,根据图象计算: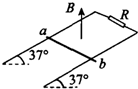 如图所示,光滑的长平行金属导轨宽度d=50cm,导轨所在的平面与水平面夹角为37°,导轨上端电阻R=0.8Ω,其他电阻不计,导轨放在竖直向上的匀强磁场中,磁感应强度B=0.4T.金属棒ab从上端由静止开始下滑,金属棒ab的质量m=0.1kg.(sin37°=0.6,cos37°=0.8,g=10m/s2) 求:
如图所示,光滑的长平行金属导轨宽度d=50cm,导轨所在的平面与水平面夹角为37°,导轨上端电阻R=0.8Ω,其他电阻不计,导轨放在竖直向上的匀强磁场中,磁感应强度B=0.4T.金属棒ab从上端由静止开始下滑,金属棒ab的质量m=0.1kg.(sin37°=0.6,cos37°=0.8,g=10m/s2) 求: 如图所示,在光滑的水平面上有A、B两辆质量均为m的小车,保持静止状态,A车上站着一个质量为$\frac{m}{2}$的人,当人从A车跳到B车上,并与B车保持相对静止,则A车与B车速度大小比等于3:2.
如图所示,在光滑的水平面上有A、B两辆质量均为m的小车,保持静止状态,A车上站着一个质量为$\frac{m}{2}$的人,当人从A车跳到B车上,并与B车保持相对静止,则A车与B车速度大小比等于3:2.