题目内容
11.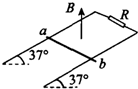 如图所示,光滑的长平行金属导轨宽度d=50cm,导轨所在的平面与水平面夹角为37°,导轨上端电阻R=0.8Ω,其他电阻不计,导轨放在竖直向上的匀强磁场中,磁感应强度B=0.4T.金属棒ab从上端由静止开始下滑,金属棒ab的质量m=0.1kg.(sin37°=0.6,cos37°=0.8,g=10m/s2) 求:
如图所示,光滑的长平行金属导轨宽度d=50cm,导轨所在的平面与水平面夹角为37°,导轨上端电阻R=0.8Ω,其他电阻不计,导轨放在竖直向上的匀强磁场中,磁感应强度B=0.4T.金属棒ab从上端由静止开始下滑,金属棒ab的质量m=0.1kg.(sin37°=0.6,cos37°=0.8,g=10m/s2) 求:(1)求导体棒下滑速度为5m/s时通过电阻R的电流大小;
(2)求导体棒下滑的最大速度;
(3)若经过时间t,导体棒下滑的垂直距离为h,速度为v,若在同一时间内,电阻产生的热与一恒定电流I0在该电阻上产生的热相同,求恒定电流I0的表达式(各物理量全部用字母表示).
分析 (1)根据法拉第电磁感应定律与闭合电路欧姆定律,即可求解;
(2)由安培力公式求出安培力,然后由平衡条件求出最大速度;
(3)由能量守恒定律与焦耳定律分析答题.
解答 解:(1)由法拉第电磁感应定律:E=Bdvcos37°=0.8v
由闭合电路欧姆定律:$I=\frac{E}{R}=1A$
(2)导体棒速度最大时处于匀速运动状态,
导体棒受到的安培力:${F_安}=BId=\frac{{{B^2}{L^2}{v_m}cosθ}}{R}$
导体棒匀速运动时,受力是平衡的:mgtanθ=F安
得:vm=18.75m/s
(3)由能量守恒定律得:$mgh=\frac{1}{2}m{v^2}+Q$
由焦耳定律得:$Q=I_0^2Rt$
联立解得:${I_0}=\sqrt{\frac{{mgh-\frac{1}{2}m{v^2}}}{Rt}}$
答:(1)导体棒下滑速度为5m/s时通过电阻R的电流大小1A;
(2)导体棒下滑的最大速度18.75m/s;
(3)恒定电流的表达式${I_0}=\sqrt{\frac{{mgh-\frac{1}{2}m{v^2}}}{Rt}}$.
点评 考查受力分析的方法,掌握法拉第电磁感应定律与闭合电路欧姆定律的应用,理解牛顿第二定律的运用.注意速度最大时,加速度为零,处于平衡状态.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
1.如图所示,通电导线旁边同一平面有矩形线圈a则( )
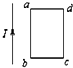

| A. | 若线圈向右平动,其中感应电流方向是a→b→c→d→a | |
| B. | 当线圈向导线靠近时,无感应电流产生 | |
| C. | 当线圈从图示位置以ab边为轴转动时,其中感应电流方向是a→b→c→d→a | |
| D. | 若线圈竖直向下平动,无感应电流产生 |
2.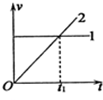 平抛运动可以分解为水平和竖直两个方向的直线运动,在同一坐标系中作出这两个分运动的v-t图象,如图所示,若平抛运动的时间大于2t1,则下列说法中正确的是( )
平抛运动可以分解为水平和竖直两个方向的直线运动,在同一坐标系中作出这两个分运动的v-t图象,如图所示,若平抛运动的时间大于2t1,则下列说法中正确的是( )
 平抛运动可以分解为水平和竖直两个方向的直线运动,在同一坐标系中作出这两个分运动的v-t图象,如图所示,若平抛运动的时间大于2t1,则下列说法中正确的是( )
平抛运动可以分解为水平和竖直两个方向的直线运动,在同一坐标系中作出这两个分运动的v-t图象,如图所示,若平抛运动的时间大于2t1,则下列说法中正确的是( )| A. | 图线2表示竖直分运动的v-t图线 | |
| B. | t1时间内的竖直位移与水平位移之比为1:1 | |
| C. | t1时刻的速度方向与初速度方向夹角为45° | |
| D. | 2t1时刻的速度方向与初速度方向的夹角为45° |
6.某水力发电站的发电机有稳定的输出电压,它发出的电先通过附近的变压器升压,然后通过高压输电线路把电能输送到远处村寨附近的降压变压器,经降压后再送入村寨中各用户.设变压器都是理想的,则随着村寨中接入电路的用电器消耗的总功率的增加,则( )
| A. | 通过升压变压器初级线圈中的电流变大 | |
| B. | 升压变压器次级线圈两端的电压变小 | |
| C. | 高压输电线路上的电压损失变大 | |
| D. | 降压变压器次级线圈两端的电压变小 |
3. 如图,A,B两等量异号点电荷,在A,B连线上有a,b,c三点,其中b为连线的中点,ab=bc,若规定无穷远处电势为零,则( )
如图,A,B两等量异号点电荷,在A,B连线上有a,b,c三点,其中b为连线的中点,ab=bc,若规定无穷远处电势为零,则( )
 如图,A,B两等量异号点电荷,在A,B连线上有a,b,c三点,其中b为连线的中点,ab=bc,若规定无穷远处电势为零,则( )
如图,A,B两等量异号点电荷,在A,B连线上有a,b,c三点,其中b为连线的中点,ab=bc,若规定无穷远处电势为零,则( )| A. | a点与c点的电场强度相同 | |
| B. | a点与c点的电势相同 | |
| C. | b点电势为零 | |
| D. | 点电荷q沿A、B连线的中垂线移动,电场力不做功,电势能不改变 |
20.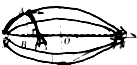 如图所示,两个等量异种电荷固定在M、N两点,O是MN的中点,A、B是平面电场中的两点,AB垂直于MN,有甲乙两个相同的带电粒子分别从A、B两点以平行于MN的相同速度开始运动,随后两粒子都能从左向右经过O点,则以下说法正确的是( )
如图所示,两个等量异种电荷固定在M、N两点,O是MN的中点,A、B是平面电场中的两点,AB垂直于MN,有甲乙两个相同的带电粒子分别从A、B两点以平行于MN的相同速度开始运动,随后两粒子都能从左向右经过O点,则以下说法正确的是( )
 如图所示,两个等量异种电荷固定在M、N两点,O是MN的中点,A、B是平面电场中的两点,AB垂直于MN,有甲乙两个相同的带电粒子分别从A、B两点以平行于MN的相同速度开始运动,随后两粒子都能从左向右经过O点,则以下说法正确的是( )
如图所示,两个等量异种电荷固定在M、N两点,O是MN的中点,A、B是平面电场中的两点,AB垂直于MN,有甲乙两个相同的带电粒子分别从A、B两点以平行于MN的相同速度开始运动,随后两粒子都能从左向右经过O点,则以下说法正确的是( )| A. | 两个粒子均带正电 | |
| B. | 甲粒子在A处的加速度比乙粒子在B处的加速度大 | |
| C. | 甲粒子在O点的动能大于乙粒子在O点的动能 | |
| D. | 甲粒子从A点到O点经历的时间比乙粒子从B点到O点的时间短 |
1.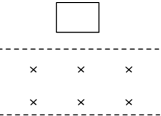 如图所示,在一个左右延伸很远的上、下有界的匀强磁场上方有一闭合线圈,当闭合线圈从上方下落穿过磁场的过程中( )
如图所示,在一个左右延伸很远的上、下有界的匀强磁场上方有一闭合线圈,当闭合线圈从上方下落穿过磁场的过程中( )
 如图所示,在一个左右延伸很远的上、下有界的匀强磁场上方有一闭合线圈,当闭合线圈从上方下落穿过磁场的过程中( )
如图所示,在一个左右延伸很远的上、下有界的匀强磁场上方有一闭合线圈,当闭合线圈从上方下落穿过磁场的过程中( )| A. | 进入磁场时加速度可能小于g,离开磁场时加速度可能大于g,也可能小于g | |
| B. | 进入磁场时加速度大于g,离开时小于g | |
| C. | 进入磁场和离开磁场,加速度都大于g | |
| D. | 进入磁场和离开磁场,加速度都小于g |
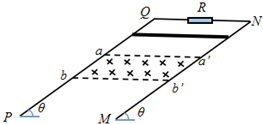 如图所示,两根平行的光滑的金属导轨PQ和MN相距L,它们与水平方向的夹角为θ,导轨的上方跟电阻R相连,在导轨的下端有一宽度为d(即ab=d)磁感应强度为B的有界匀强磁场,磁场的边界aa′和bb′垂直于导轨,磁场的方向与导轨平面垂直,质量为m的电阻不计的导体棒从某位置静止释放,恰好能匀速地通过磁场区域.若当地的重力加速度为g,求:
如图所示,两根平行的光滑的金属导轨PQ和MN相距L,它们与水平方向的夹角为θ,导轨的上方跟电阻R相连,在导轨的下端有一宽度为d(即ab=d)磁感应强度为B的有界匀强磁场,磁场的边界aa′和bb′垂直于导轨,磁场的方向与导轨平面垂直,质量为m的电阻不计的导体棒从某位置静止释放,恰好能匀速地通过磁场区域.若当地的重力加速度为g,求: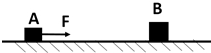 如图所示,光滑水平面上静止放置两物体A、B,mA=1kg,mB=2kg.现对A施加一个水平向右的恒力F=3N,经时间t=3s后撤去该力.A继续运动一段时间后,与B发生正碰,碰后A、B粘在一起以共同的速度向右运动.求:
如图所示,光滑水平面上静止放置两物体A、B,mA=1kg,mB=2kg.现对A施加一个水平向右的恒力F=3N,经时间t=3s后撤去该力.A继续运动一段时间后,与B发生正碰,碰后A、B粘在一起以共同的速度向右运动.求: