题目内容
19.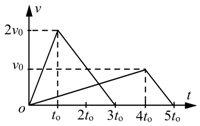 质量相等的A、B两物体放在同一水平面上,分别受到水平拉力F1、F2的作用而从静止开始做匀加速直线运动.经过时间t0和4t0速度分别达到2v0和v0时,分别撤去F1和F2,以后物体继续做匀减速直线运动直至停止.两物体速度随时间变化的图线如图所示.设F1和F2对A、B的冲量分别为I1和I2,F1和F2对A、B做的功分别为W1和W2,则下列结论正确的是( )
质量相等的A、B两物体放在同一水平面上,分别受到水平拉力F1、F2的作用而从静止开始做匀加速直线运动.经过时间t0和4t0速度分别达到2v0和v0时,分别撤去F1和F2,以后物体继续做匀减速直线运动直至停止.两物体速度随时间变化的图线如图所示.设F1和F2对A、B的冲量分别为I1和I2,F1和F2对A、B做的功分别为W1和W2,则下列结论正确的是( )| A. | I1:I2=12:5,W1:W2=6:5 | B. | I1:I2=6:5,W1:W2=3:5 | ||
| C. | I1:I2=3:5,W1:W2=6:5 | D. | I1:I2=3:5,W1:W2=12:5 |
分析 明确图象的性质,根据图象的斜率可求得加速度关系,注意减速过程加速度相同,根据牛顿第二定律可明确摩擦力大小,同理可求得拉力大小,再由冲量的定义可求得冲量关系;
根据图象可明确位移关系,再根据动能定理即可求得牵引力的功.
解答 解:从图象可知,两物块匀减速运动的加速度大小之都为a=$\frac{v_{0}}{t_{0}}$,根据牛顿第二定律,匀减速运动中有f=ma,则摩擦力大小都为f=m$\frac{v_{0}}{t_{0}}$.根据图象知,匀加速运动的加速度分别为:$\frac{2v_{0}}{t_{0}}$,$\frac{v_{0}}{4t_{0}}$,根据牛顿第二定律,匀加速运动中有F-f=ma,则F1=$\frac{3mv_{0}}{t_{0}}$,F2=$\frac{5mv_{0}}{4t_{0}}$,F1和F2的大小之比为12:5.则冲量之比为:I1:I2=$\frac{12}{5}$×$\frac{{t}_{0}}{4{t}_{0}}$=$\frac{3}{5}$
图线与时间轴所围成的面积表示运动的位移,则位移之比为6:5;由图看出,撤去拉力后两图象平行,说明加速度,由牛顿第二定律分析则知加速度a=μg,说明两物体与地面的动摩擦因数相等,则两物体所受的摩擦力大小相等,设为f,对全过程运用动能定理得:
W1-fs1=0,W2-fs2=0,得:W1=fs1,W2=fs2,由上可知,整个运动过程中F1和F2做功之比为6:5;
故C正确,ABD错误.
故选:C.
点评 解决本题的关键通过图象得出匀加速运动和匀减速运动的加速度,根据牛顿第二定律,得出两个力的大小之比,以及知道速度-时间图线与时间轴所围成的面积表示位移,同时能正确利用动能定理和动量定理进行分析求解.

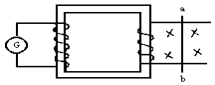 两个线圈A、B绕在一个铁芯的两侧,分别跟电流表和导轨相连,导轨上垂直搁置一根金属棒ab,垂直导轨平面有一个匀强磁场,如图所示.在下列情况下能使电流计中有电流通过的是( )
两个线圈A、B绕在一个铁芯的两侧,分别跟电流表和导轨相连,导轨上垂直搁置一根金属棒ab,垂直导轨平面有一个匀强磁场,如图所示.在下列情况下能使电流计中有电流通过的是( )| A. | ab向右作匀速运动 | B. | ab向左作匀速运动 | ||
| C. | ab向竖直方向作加速运动 | D. | ab向左作加速运动 |
| A. | 有时人们感到空气干燥,这是由于空气相对于湿度小的缘故 | |
| B. | 所有晶体沿各个方向的物理性质、化学性质和光学性质都相同 | |
| C. | 气体能充满任何容器是因为分子间的排斥力大于吸引力 | |
| D. | 当分子力表现为引力时,分子势能随分子间距离的增大而增大 | |
| E. | 能量耗散是从能量转化的角度反映出自然界中的宏观过程具有方向性 |
| A. | 天然放射现象的发现,揭示了原子核是由质子和中子组成的 | |
| B. | 氢原子的能级理论是玻尔在卢瑟福核式结构模型的基础上提出来的 | |
| C. | 汤姆孙通过对阴极射线的研究提出了原子核具有复杂的结构 | |
| D. | 卢瑟福的α粒子散射实验揭示了原子只能处于一系列不连续的能量状态中 |
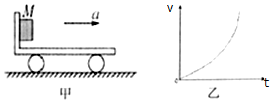
| A. | 物块所受摩擦力减小 | |
| B. | 物块所受摩擦力增大 | |
| C. | 车厢对物块的作用力大小增大且方向改变 | |
| D. | 车厢对物块的作用力大小增大但方向不变 |
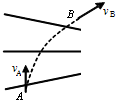 某电场的电场线分布如图实线所示,一带电粒子在电场力作用下经A点运动到B点,运动轨迹如虚线所示,粒子重力不计,则粒子的加速度、动能、电势能的变化情况是( )
某电场的电场线分布如图实线所示,一带电粒子在电场力作用下经A点运动到B点,运动轨迹如虚线所示,粒子重力不计,则粒子的加速度、动能、电势能的变化情况是( )| A. | 若粒子带正电,其加速度和动能都增大,A、B两点电势差UAB<0 | |
| B. | 若粒子带正电,其动能增大,加速度和电势能都减小 | |
| C. | 若粒子带负电,其加速度和动能都增大,电势降低 | |
| D. | 若粒子带负电,其加速度和动能都增大,电势能减小 |
 如图所示,质量相同的两个带电粒子M、N以相同的速度同时沿垂直于电场方向射入两平行板间的匀强电场中,M从两极板正中央射入,N从下极板边缘处射入,它们最后打在同一点.不计带电粒子重力和带电粒子间的相互作用,则从开始射入到打在上极板的过程中( )
如图所示,质量相同的两个带电粒子M、N以相同的速度同时沿垂直于电场方向射入两平行板间的匀强电场中,M从两极板正中央射入,N从下极板边缘处射入,它们最后打在同一点.不计带电粒子重力和带电粒子间的相互作用,则从开始射入到打在上极板的过程中( )| A. | 它们运动的时间tN=tM | |
| B. | 它们电势能减少量之比△EM:△EN=1:2 | |
| C. | 它们的动能增量之比△EkM:△EkN=1:2 | |
| D. | 它们所带的电荷量之比qM:qN=1:2 |
 质量为m的小球由轻绳a和b系于一轻质木架上的A点和C点,如图所示.当轻杆绕轴BC以角速度ω匀速转动时,小球在水平面内作匀速圆周运动,绳a在竖直方向、绳b在水平方向.当小球运动到图示位置时.绳b被烧断,同时杆也停止转动,则( )
质量为m的小球由轻绳a和b系于一轻质木架上的A点和C点,如图所示.当轻杆绕轴BC以角速度ω匀速转动时,小球在水平面内作匀速圆周运动,绳a在竖直方向、绳b在水平方向.当小球运动到图示位置时.绳b被烧断,同时杆也停止转动,则( )| A. | 小球仍在水平面内作匀速圆周运动 | |
| B. | 在绳被烧断瞬间,a绳中张力突然减小 | |
| C. | 若角速度ω较小,小球在垂直于平面ABC的竖直平面内摆动 | |
| D. | 若角速度ω较大,小球可以在垂直于平面ABC的竖直平面内作圆周运动 |
 如图所示,足够长且电阻不计的光滑导轨PQ、MN相距d=1m,其与水平面夹角为α,整个导轨所在区域有匀强磁场,磁场方向垂直于导轨平面斜向上;长为1m的金属棒ab垂直于导轨放置,且接触良好,金属棒质量为0.1kg且电阻r=1Ω;导轨右侧电路中灯泡的电阻RL=3Ω、定值电阻R1=7Ω;现调节电阻箱使R2=6Ω,在t=0时刻由静止释放ab,t=0.25s时刻闭合开关S,此时金属棒的速度v1=1.5m/s,此后ab棒做变加速运动且最终以v2=6m/s做匀速直线运动,重力加速度大小g=10m/s2.
如图所示,足够长且电阻不计的光滑导轨PQ、MN相距d=1m,其与水平面夹角为α,整个导轨所在区域有匀强磁场,磁场方向垂直于导轨平面斜向上;长为1m的金属棒ab垂直于导轨放置,且接触良好,金属棒质量为0.1kg且电阻r=1Ω;导轨右侧电路中灯泡的电阻RL=3Ω、定值电阻R1=7Ω;现调节电阻箱使R2=6Ω,在t=0时刻由静止释放ab,t=0.25s时刻闭合开关S,此时金属棒的速度v1=1.5m/s,此后ab棒做变加速运动且最终以v2=6m/s做匀速直线运动,重力加速度大小g=10m/s2.