题目内容
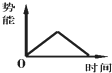
15. 如图甲所示,MN左侧有一垂直纸面向里的匀强磁场.现将一边长为l、质量为m、电阻为R的正方形金属线框置于该磁场中,使线框平面与磁铁场垂直,且bc边与磁场边界MN重合.当t=t0时,对线框的ad边与磁场边界MN重合.图乙为拉力F随时间变化的图线.由以上条件可知,磁场的磁感应强度B的大小为( )
如图甲所示,MN左侧有一垂直纸面向里的匀强磁场.现将一边长为l、质量为m、电阻为R的正方形金属线框置于该磁场中,使线框平面与磁铁场垂直,且bc边与磁场边界MN重合.当t=t0时,对线框的ad边与磁场边界MN重合.图乙为拉力F随时间变化的图线.由以上条件可知,磁场的磁感应强度B的大小为( )| A. | B=$\frac{1}{l}$$\sqrt{\frac{mR}{{t}_{0}}}$ | B. | B=$\frac{1}{l}$$\sqrt{\frac{2mR}{{t}_{0}}}$ | C. | B=$\frac{2}{l}$$\sqrt{\frac{mR}{2{t}_{0}}}$ | D. | B=$\frac{2}{l}$$\sqrt{\frac{mR}{{t}_{0}}}$ |
分析 t=0时刻,感应电流为零,线框受到的安培力为零.由牛顿第二定律可求出加速度,并求出t0时刻线框的速率v.当t=t0时,由图读出拉力,根据牛顿第二定律列出表达式,结合斜率求出
解答  解:t=0时刻,感应电动势 E=0,感应电流 I=0,线圈所受的安培力 F安=BIl=0,
解:t=0时刻,感应电动势 E=0,感应电流 I=0,线圈所受的安培力 F安=BIl=0,
由牛顿第二定律得:F0=ma,得 a=$\frac{{F}_{0}}{m}$
t=t0时线圈的速度为 v=at0=$\frac{{F}_{0}{t}_{0}}{m}$
根据牛顿第二定律得,F-F安=ma
又F安=BIl,I=$\frac{E}{R}$,E=Blv,
得到 F=$\frac{{B}^{2}{l}^{2}a}{R}$t+ma
由图读出图线的斜率K=$\frac{2{F}_{0}}{{t}_{0}}$=$\frac{{B}^{2}{l}^{2}a}{R}$=$\frac{{B}^{2}{l}^{2}}{R}$$•\frac{{F}_{0}}{m}$
解得B=$\frac{1}{l}$$\sqrt{\frac{2mR}{{t}_{0}}}$
故选:B.
点评 本题的关键求出安培力,列出牛顿第二定律关于B的表达式,要有读图的能力.这里要知道安培力是联系力学与电磁感应的桥梁.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
5. 如图所示,带箭头的线表示某一电场的电场线,只在电场力作用下,一带电粒子经A点飞向B点,径迹如图中虚线所示,下列说法正确的是 ( )
如图所示,带箭头的线表示某一电场的电场线,只在电场力作用下,一带电粒子经A点飞向B点,径迹如图中虚线所示,下列说法正确的是 ( )
 如图所示,带箭头的线表示某一电场的电场线,只在电场力作用下,一带电粒子经A点飞向B点,径迹如图中虚线所示,下列说法正确的是 ( )
如图所示,带箭头的线表示某一电场的电场线,只在电场力作用下,一带电粒子经A点飞向B点,径迹如图中虚线所示,下列说法正确的是 ( )| A. | 粒子带正电 | B. | 粒子在A点电势能大 | ||
| C. | 粒子在B点动能大 | D. | A、B两点相比,B点电势较低 |
6.下列有关电源电动势的说法中正确的是( )
| A. | 电源的电动势在数值上等于不接用电器时电源正、负极间的电压 | |
| B. | 把同一电源接在不同的电路中,电源的电动势将保持不变 | |
| C. | 电源的电动势就是电压 | |
| D. | 电动势、电压和电势差虽名称不同,但物理意义相同,所以单位也相同 |
3. 一质量为m的小球套在倾斜放置的固定光滑杆上,一根轻质弹簧的一端悬挂于O点,另一端与小球相连,弹簧与杆在同一竖直平面内,将小球沿杆拉到与弹簧水平的位置由静止释放,小球沿杆下滑,当弹簧位于竖直位置时,小球速度恰好为零,此时小球下降的竖直高度为h,如图所示.若全过程中弹簧处于伸长状态且处于弹性限度内,重力加速度为g,则下列说法正确的是( )
一质量为m的小球套在倾斜放置的固定光滑杆上,一根轻质弹簧的一端悬挂于O点,另一端与小球相连,弹簧与杆在同一竖直平面内,将小球沿杆拉到与弹簧水平的位置由静止释放,小球沿杆下滑,当弹簧位于竖直位置时,小球速度恰好为零,此时小球下降的竖直高度为h,如图所示.若全过程中弹簧处于伸长状态且处于弹性限度内,重力加速度为g,则下列说法正确的是( )
 一质量为m的小球套在倾斜放置的固定光滑杆上,一根轻质弹簧的一端悬挂于O点,另一端与小球相连,弹簧与杆在同一竖直平面内,将小球沿杆拉到与弹簧水平的位置由静止释放,小球沿杆下滑,当弹簧位于竖直位置时,小球速度恰好为零,此时小球下降的竖直高度为h,如图所示.若全过程中弹簧处于伸长状态且处于弹性限度内,重力加速度为g,则下列说法正确的是( )
一质量为m的小球套在倾斜放置的固定光滑杆上,一根轻质弹簧的一端悬挂于O点,另一端与小球相连,弹簧与杆在同一竖直平面内,将小球沿杆拉到与弹簧水平的位置由静止释放,小球沿杆下滑,当弹簧位于竖直位置时,小球速度恰好为零,此时小球下降的竖直高度为h,如图所示.若全过程中弹簧处于伸长状态且处于弹性限度内,重力加速度为g,则下列说法正确的是( )| A. | 当弹簧与杆垂直时,小球动能最大 | |
| B. | 当小球沿杆下滑过程中合力为零时,小球速度为0 | |
| C. | 在小球自开始下滑至滑到最低点的过程中,弹簧所做的负功小于mgh | |
| D. | 在小球自开始下滑至滑到最低点的过程中,弹簧弹性势能的增加量等于mgh |
7. 在用盛沙漏斗演示简谐运动时,当薄木板匀速地拉动时,摆动的漏斗中漏出的沙子在板上形成的曲线显示出摆的位移随时间变化的关系.板上OO′代表时间轴.下图是两个摆中的沙子在各自木板上形成的曲线.若板1和板2拉动的速度v1和v2的关系为v2=2v1,则板1和板2上曲线所代表的振动周期T1和T2的关系为( )
在用盛沙漏斗演示简谐运动时,当薄木板匀速地拉动时,摆动的漏斗中漏出的沙子在板上形成的曲线显示出摆的位移随时间变化的关系.板上OO′代表时间轴.下图是两个摆中的沙子在各自木板上形成的曲线.若板1和板2拉动的速度v1和v2的关系为v2=2v1,则板1和板2上曲线所代表的振动周期T1和T2的关系为( )
 在用盛沙漏斗演示简谐运动时,当薄木板匀速地拉动时,摆动的漏斗中漏出的沙子在板上形成的曲线显示出摆的位移随时间变化的关系.板上OO′代表时间轴.下图是两个摆中的沙子在各自木板上形成的曲线.若板1和板2拉动的速度v1和v2的关系为v2=2v1,则板1和板2上曲线所代表的振动周期T1和T2的关系为( )
在用盛沙漏斗演示简谐运动时,当薄木板匀速地拉动时,摆动的漏斗中漏出的沙子在板上形成的曲线显示出摆的位移随时间变化的关系.板上OO′代表时间轴.下图是两个摆中的沙子在各自木板上形成的曲线.若板1和板2拉动的速度v1和v2的关系为v2=2v1,则板1和板2上曲线所代表的振动周期T1和T2的关系为( )| A. | T2=T1 | B. | T2=$\frac{{T}_{1}}{4}$ | C. | T2=4T1 | D. | T2=2T1 |
4.下面说法中正确的是( )
| A. | 曲线运动一定是变速运动 | |
| B. | 平抛运动一定是匀变速运动 | |
| C. | 匀速圆周运动一定是速度不变的运动 | |
| D. | 当物体受到的合外力减小时,物体的速度一定减小 |
 两根足够长的平行金属导轨,固定在同一水平面上,磁感应强度B=0.50T的匀强磁场与导轨所在平面垂直,导轨的电阻很小,可不计.导轨间的距离ι=0.20m.两根质量均为m=0.10kg的平行杆甲、乙可在导轨上无摩擦地滑动,滑动过程中与导轨保持垂直,每根金属杆的电阻均为R=0.50Ω,在t=0时刻,两杆都处于静止状态.现有一与导轨平行,大小为0.20N的力F作用于金属杆甲上,使金属杆在导轨上滑动.经过t=5.0s,金属杆甲的加速度a=1.37m/s2,问此时两金属杆的速度各为多少?
两根足够长的平行金属导轨,固定在同一水平面上,磁感应强度B=0.50T的匀强磁场与导轨所在平面垂直,导轨的电阻很小,可不计.导轨间的距离ι=0.20m.两根质量均为m=0.10kg的平行杆甲、乙可在导轨上无摩擦地滑动,滑动过程中与导轨保持垂直,每根金属杆的电阻均为R=0.50Ω,在t=0时刻,两杆都处于静止状态.现有一与导轨平行,大小为0.20N的力F作用于金属杆甲上,使金属杆在导轨上滑动.经过t=5.0s,金属杆甲的加速度a=1.37m/s2,问此时两金属杆的速度各为多少? 如图,是马戏团中上演的飞车节目,在竖直平面内有半径为R的圆轨道.表演者骑着摩托车在固定的圆轨道内做圆周运动.已知人和摩托车的总质量为m,人以v1=$\sqrt{2gR}$的速度过轨道最高点B,并以v2=$\sqrt{3}$v1的速度过最低点A.
如图,是马戏团中上演的飞车节目,在竖直平面内有半径为R的圆轨道.表演者骑着摩托车在固定的圆轨道内做圆周运动.已知人和摩托车的总质量为m,人以v1=$\sqrt{2gR}$的速度过轨道最高点B,并以v2=$\sqrt{3}$v1的速度过最低点A.