��Ŀ����
3�� һ����Ϊm��С��������б���õĹ̶��⻬���ϣ�һ�����ʵ��ɵ�һ��������O�㣬��һ����С�����������������ͬһ��ֱƽ���ڣ���С���ظ������뵯��ˮƽ��λ���ɾ�ֹ�ͷţ�С���ظ��»���������λ����ֱλ��ʱ��С���ٶ�ǡ��Ϊ�㣬��ʱС���½�����ֱ�߶�Ϊh����ͼ��ʾ����ȫ�����е��ɴ����쳤״̬�Ҵ��ڵ������ڣ��������ٶ�Ϊg��������˵����ȷ���ǣ�������
һ����Ϊm��С��������б���õĹ̶��⻬���ϣ�һ�����ʵ��ɵ�һ��������O�㣬��һ����С�����������������ͬһ��ֱƽ���ڣ���С���ظ������뵯��ˮƽ��λ���ɾ�ֹ�ͷţ�С���ظ��»���������λ����ֱλ��ʱ��С���ٶ�ǡ��Ϊ�㣬��ʱС���½�����ֱ�߶�Ϊh����ͼ��ʾ����ȫ�����е��ɴ����쳤״̬�Ҵ��ڵ������ڣ��������ٶ�Ϊg��������˵����ȷ���ǣ�������| A�� | ��������˴�ֱʱ��С������� | |
| B�� | ��С���ظ��»������к���Ϊ��ʱ��С���ٶ�Ϊ0 | |
| C�� | ��С���Կ�ʼ�»���������͵�Ĺ����У����������ĸ���С��mgh | |
| D�� | ��С���Կ�ʼ�»���������͵�Ĺ����У����ɵ������ܵ�����������mgh |
���� ������˴�ֱʱ�������������ظ����£�С��������٣��ٶ�û�дﵽ���ֵ���˶������У�ֻ�������͵��ɵ���������ϵͳ��е���غ㣬���ݻ�е���غ㶨�ɷ����������
��� �⣺AB��������˴�ֱʱ������������˴�ֱ�������������ظ����£�С��������٣��ٶ�û�дﵽ���ֵ����������Ϊ��ʱ�����ٶ�Ϊ�㣬�ٶ����A����B����
CD��С���˶������У�ֻ�������͵��ɵ���������ϵͳ��е���غ㣬��ĩλ�ö��ܶ�Ϊ�㣬���Ե��ɵĵ������������������������ܵļ�С������Ϊmgh����C����D��ȷ��
��ѡ��D
���� ������Ҫ�����˻�е���غ㶨�ɵ�ֱ��Ӧ�ã�Ҫ��ͬѧ������ȷ����С�������������˶�������ѶȲ������ڻ����⣮

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
13�� ��ͼ��ʾ����Ϊ2L��ֱ�����۳ɱ߳���ȡ��н�Ϊ60���V�Σ���������������ƽ���ഹֱ����ǿ�ų��У��ų��ĴŸ�Ӧǿ��ΪB�����ڸõ�����ͨ�Դ�СΪI�ĵ���ʱ����V��ͨ�絼���ܵ��İ�������СΪ ��������
��ͼ��ʾ����Ϊ2L��ֱ�����۳ɱ߳���ȡ��н�Ϊ60���V�Σ���������������ƽ���ഹֱ����ǿ�ų��У��ų��ĴŸ�Ӧǿ��ΪB�����ڸõ�����ͨ�Դ�СΪI�ĵ���ʱ����V��ͨ�絼���ܵ��İ�������СΪ ��������
 ��ͼ��ʾ����Ϊ2L��ֱ�����۳ɱ߳���ȡ��н�Ϊ60���V�Σ���������������ƽ���ഹֱ����ǿ�ų��У��ų��ĴŸ�Ӧǿ��ΪB�����ڸõ�����ͨ�Դ�СΪI�ĵ���ʱ����V��ͨ�絼���ܵ��İ�������СΪ ��������
��ͼ��ʾ����Ϊ2L��ֱ�����۳ɱ߳���ȡ��н�Ϊ60���V�Σ���������������ƽ���ഹֱ����ǿ�ų��У��ų��ĴŸ�Ӧǿ��ΪB�����ڸõ�����ͨ�Դ�СΪI�ĵ���ʱ����V��ͨ�絼���ܵ��İ�������СΪ ��������| A�� | 0 | B�� | BIL | C�� | $\frac{1}{2}$BIL | D�� | $\frac{\sqrt{3}}{2}$BIL |
11���������������������ٴ������ӵ�װ�ã�����IJ����Ƿֱ���߶�������������ӵ�����D�ν����У��ںм���������γɵ������Ա仯����ǿ�糡��ʹ����������ͨ������ʱ���ܱ����٣���D�ͽ����д��ڴ�ֱ�ںе������ǿ�ų��У�������˵������ȷ���ǣ�������
| A�� | �������ӴӴų�������� | |
| B�� | �������ӴӼ������ı�Ե��������� | |
| C�� | �������ӴӼ����������ĸ������������ | |
| D�� | �����������������ǿ�糡�ĵ糡ǿ�ȣ������������������ʱ�Ķ��ܾ����� |
15�� ��ͼ����ʾ��MN�����һ��ֱֽ���������ǿ�ų����ֽ�һ�߳�Ϊl������Ϊm������ΪR�������ν����߿����ڸôų��У�ʹ�߿�ƽ�����������ֱ����bc����ų��߽�MN�غϣ���t=t0ʱ�����߿��ad����ų��߽�MN�غϣ�ͼ��Ϊ����F��ʱ��仯��ͼ�ߣ�������������֪���ų��ĴŸ�Ӧǿ��B�Ĵ�СΪ��������
��ͼ����ʾ��MN�����һ��ֱֽ���������ǿ�ų����ֽ�һ�߳�Ϊl������Ϊm������ΪR�������ν����߿����ڸôų��У�ʹ�߿�ƽ�����������ֱ����bc����ų��߽�MN�غϣ���t=t0ʱ�����߿��ad����ų��߽�MN�غϣ�ͼ��Ϊ����F��ʱ��仯��ͼ�ߣ�������������֪���ų��ĴŸ�Ӧǿ��B�Ĵ�СΪ��������
 ��ͼ����ʾ��MN�����һ��ֱֽ���������ǿ�ų����ֽ�һ�߳�Ϊl������Ϊm������ΪR�������ν����߿����ڸôų��У�ʹ�߿�ƽ�����������ֱ����bc����ų��߽�MN�غϣ���t=t0ʱ�����߿��ad����ų��߽�MN�غϣ�ͼ��Ϊ����F��ʱ��仯��ͼ�ߣ�������������֪���ų��ĴŸ�Ӧǿ��B�Ĵ�СΪ��������
��ͼ����ʾ��MN�����һ��ֱֽ���������ǿ�ų����ֽ�һ�߳�Ϊl������Ϊm������ΪR�������ν����߿����ڸôų��У�ʹ�߿�ƽ�����������ֱ����bc����ų��߽�MN�غϣ���t=t0ʱ�����߿��ad����ų��߽�MN�غϣ�ͼ��Ϊ����F��ʱ��仯��ͼ�ߣ�������������֪���ų��ĴŸ�Ӧǿ��B�Ĵ�СΪ��������| A�� | B=$\frac{1}{l}$$\sqrt{\frac{mR}{{t}_{0}}}$ | B�� | B=$\frac{1}{l}$$\sqrt{\frac{2mR}{{t}_{0}}}$ | C�� | B=$\frac{2}{l}$$\sqrt{\frac{mR}{2{t}_{0}}}$ | D�� | B=$\frac{2}{l}$$\sqrt{\frac{mR}{{t}_{0}}}$ |
 ��ͼ��ʾ��������λ��ͬһ��ֱƽ���ڵ�ˮƽ��������������������A��B������ͨ��һ���ƹ������ֵIJ����쳤�����������ӣ�����A��������vA�˶��������������ɽǶȦ�ʱ������B���ٶȴ�СvBΪ$\frac{{v}_{A}}{cos��}$��
��ͼ��ʾ��������λ��ͬһ��ֱƽ���ڵ�ˮƽ��������������������A��B������ͨ��һ���ƹ������ֵIJ����쳤�����������ӣ�����A��������vA�˶��������������ɽǶȦ�ʱ������B���ٶȴ�СvBΪ$\frac{{v}_{A}}{cos��}$��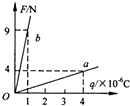 ��oxy����ϵ������ԭ��O���̶�һ����Q������̽���q�Ⱥ����Oxy����ϵ�е�A��B���㣬��֪A��������ԭ��O֮��ľ���Ϊ30cm������A��B�������̽��������������С���糡���Ĵ�С�Ĺ�ϵ��ͼֱ��a��b��ʾ����
��oxy����ϵ������ԭ��O���̶�һ����Q������̽���q�Ⱥ����Oxy����ϵ�е�A��B���㣬��֪A��������ԭ��O֮��ľ���Ϊ30cm������A��B�������̽��������������С���糡���Ĵ�С�Ĺ�ϵ��ͼֱ��a��b��ʾ���� ��1����ͼ��ʾ��Ϊʾ������壬������ʾ����һ���Ⱥܵ͡������ϴ���ģ������IJ��Σ�
��1����ͼ��ʾ��Ϊʾ������壬������ʾ����һ���Ⱥܵ͡������ϴ���ģ������IJ��Σ�