题目内容
13.某同学利用如图甲所示的装置验证动能定理.固定并调整斜槽,使它的末端O点的切线水平,在水平地面上依次铺放好木板、白纸、复写纸.将小球从不同的标记点由静止释放,记录小球到达斜槽底端时下落的高度H,并根据落点位置测量出小球平抛的水平位移x,改变小球在斜槽上的释放位置,进行多次测量,记录数据如下:| 高度H | h | 2h | 3h | 4h | 5h | 6h | 7h | 8h | 9h |
| 水平位移x | 5.5 | 9.1 | 11.7 | 14.2 | 15.9 | 17.6 | 19.0 | 20.6 | 21.7 |

(2)以H为横坐标,以x2为纵坐标,在坐标纸上描点作图,如图(乙)所示;若为一条倾斜的直线,则可以得出结论:在实验误差允许范围内,小球运动到斜槽底端的过程中,合力对小球所做的功等于小球动能的增量.
(3)受该实验方案的启发,某同学改用图丙的装置实验.他将木板竖直放置在斜槽末端的前方某一位置固定,仍将小球从不同的标记点由静止释放,记录小球到达斜槽底端时下落的高度H,并测量小球击中木板时平抛下落的高度d,他以d为纵坐标,以$\frac{1}{H}$为横坐标,描点作图,若仍为一条倾斜的直线,也达到了同样的目的.
分析 (1)小球在斜槽上滑下过程中,重力和摩擦力做功,写出合力做的功.根据平抛运动的规律求出小球离开斜槽时的速度,得到动能的变化.
(2)根据动能定理表达式,选择纵坐标.
(3)根据平抛运动的规律得到v与d的关系式,再由动能定理求得d与H的关系式,根据解析式选择纵坐标.
解答 解:(1)设小球离开斜槽时的速度为v,根据平抛运动的规律得:
x=vt,y=$\frac{1}{2}g{t}^{2}$
联立得:v=x$\sqrt{\frac{g}{2y}}$
小球在斜槽上滑下过程中,只有重力做功,则合力做的功为:W=mgH
小球动能的变化量△Ek=$\frac{1}{2}m{v}^{2}=\frac{mg{x}^{2}}{4y}$
(2)若合力对小球所做的功等于小球动能的增量,则:
mgH=$\frac{mg{x}^{2}}{4y}$,
H=$\frac{{x}^{2}}{4y}$
x2=4yH
以H为横坐标,以x2为纵坐标,在坐标纸上描点作图,若为一条倾斜的直线,则可以得出结论:在实验误差允许范围内,小球运动到斜槽底端的过程中,合力对小球所做的功等于小球动能的增量.
(3)根据平抛运动的规律有:v=$\frac{x}{t}=\frac{x}{\sqrt{\frac{2d}{g}}}=x\sqrt{\frac{g}{2d}}$
则动能定理表达式为:mgH=$\frac{1}{2}m{v}^{2}=\frac{mg{x}^{2}}{4d}$
d=$\frac{{x}^{2}}{4H}$
以d为纵坐标,以$\frac{1}{H}$为横坐标,描点作图,若仍为一条倾斜的直线,也达到了同样的目的.
故答案为:(1)mgH;$\frac{mg{x}^{2}}{4y}$;(2)x2;(3)$\frac{1}{H}$
点评 本题关键利用平抛运动的知识求得小球到达斜槽的末速度,从而写出动能定理表达式,要能根据数学知识灵活选择坐标.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案| A. | 法拉第首先提出用电场线描绘抽象的电场,这是一种形象化的研究方法 | |
| B. | 库仑得出库仑定律并用扭秤实验最早测出了元电荷e的数值 | |
| C. | 用点电荷来代替实际带电的电荷是采用了理想化物理模型的方法 | |
| D. | 场强表达式E=$\frac{F}{q}$和电势差U=$\frac{W}{q}$都是利用比值法得到的定义式 |
 滑板运动是非常受欢迎的运动,如图所示为滑板运动训练轨道简化图,装置由AB、BC、CD三段轨道组成,轨道交接处均由很小的圆弧平滑连接(图中未画出),轨道与滑板间的动摩擦因数都相同,为方便训练AB轨道可以适当调整,CD轨道固定.若运动员从A静止开始下滑则刚好能到达D,那么将AB轨道向右平移后从A正上方A1静止滑下,则( )
滑板运动是非常受欢迎的运动,如图所示为滑板运动训练轨道简化图,装置由AB、BC、CD三段轨道组成,轨道交接处均由很小的圆弧平滑连接(图中未画出),轨道与滑板间的动摩擦因数都相同,为方便训练AB轨道可以适当调整,CD轨道固定.若运动员从A静止开始下滑则刚好能到达D,那么将AB轨道向右平移后从A正上方A1静止滑下,则( )| A. | 不能到达D | |
| B. | 刚好能到达D | |
| C. | 若能经过D刚好到达D1,一定有AD∥A1D1 | |
| D. | 若能经过D刚好到达D1,但不一定有AD∥A1D1 |
 图中电容式话筒右测固定不动的金属板b与能在声波驱动下沿水平方向振动的渡 上金属层的振动膜a构成一个电容器,a、b分别通过导线与恒定电源两极相接.声源s做位移X=Asin(200πt)的振动,则有( )
图中电容式话筒右测固定不动的金属板b与能在声波驱动下沿水平方向振动的渡 上金属层的振动膜a构成一个电容器,a、b分别通过导线与恒定电源两极相接.声源s做位移X=Asin(200πt)的振动,则有( )| A. | a振动过程中a、b板之间的电场强度不变 | |
| B. | a振动过程中话筒会产生电磁波 | |
| C. | 导线ac的电流的频率为1000Hz | |
| D. | a向右位移最大时,a、b板上的电荷量最小 |
| A. | 每个分子的动能-定相间 | B. | 分子的平均速率一定相同 | ||
| C. | 分子平均动能-定相同 | D. | 内能-定相同 |
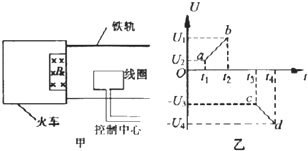 如图所示,是某高铁确定火车位置和运动状态的装置原理俯视图:能产生匀强磁场的磁铁安装在火车首节车厢下面,当它经过安放在两铁轨间的线圈时,线圈便产生一个电信号传输绐控制屮心.若火车通过线圈时,控制中心接收到线圈两端的电压信号U与时间t的关系如图乙所示,t1、t2、t3、t4是运动过程的四个时刻,则火车( )
如图所示,是某高铁确定火车位置和运动状态的装置原理俯视图:能产生匀强磁场的磁铁安装在火车首节车厢下面,当它经过安放在两铁轨间的线圈时,线圈便产生一个电信号传输绐控制屮心.若火车通过线圈时,控制中心接收到线圈两端的电压信号U与时间t的关系如图乙所示,t1、t2、t3、t4是运动过程的四个时刻,则火车( )| A. | 在t1~t2时间内做匀速直线运动 | B. | 在t1~t2时间内做匀加速直线运动 | ||
| C. | 在t3~t4时间内做匀减速直线运动 | D. | 在t3~t4时间内做匀加速直线运动 |
 用如图所示的装置可以测量磁感应强度B的值,取一长方体金属块置于匀强磁场中,磁场方向垂直于金属块前后两个侧面,左右两侧面接入电路中,测得流过长方体金属块的电流大小为I,用理想电压表测得长方体上下两表面的电势差大小为U,已知长方体金属块的长、宽、高分别为a、b、c,查得该金属材料单位体积内的自由电子数为n,电子的电荷量为e,则可以测出磁感应强度B的值为$\frac{enbU}{I}$.
用如图所示的装置可以测量磁感应强度B的值,取一长方体金属块置于匀强磁场中,磁场方向垂直于金属块前后两个侧面,左右两侧面接入电路中,测得流过长方体金属块的电流大小为I,用理想电压表测得长方体上下两表面的电势差大小为U,已知长方体金属块的长、宽、高分别为a、b、c,查得该金属材料单位体积内的自由电子数为n,电子的电荷量为e,则可以测出磁感应强度B的值为$\frac{enbU}{I}$.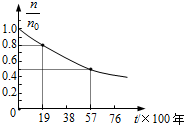 现代考古中可利用${\;}_{6}^{14}$C的衰变规律测定古生物的年代,${\;}_{6}^{14}$C衰变时放出${\;}_{-1}^{0}e$(填粒子符号),并生成新核${\;}_{7}^{14}$N.如图所示为放射性元素${\;}_{6}^{14}$C的衰变规律的示意图(纵坐标$\frac{n}{{n}_{0}}$表示的是任意时刻放射性元素的原子数与t=0时的原子数之比),则该放射性元素的半衰期是5700年.若从某次考古时发掘出来的木材中,检测到所含${\;}_{6}^{14}$C的比例是正在生长的植物中的80%,则该古物距今约1900年.
现代考古中可利用${\;}_{6}^{14}$C的衰变规律测定古生物的年代,${\;}_{6}^{14}$C衰变时放出${\;}_{-1}^{0}e$(填粒子符号),并生成新核${\;}_{7}^{14}$N.如图所示为放射性元素${\;}_{6}^{14}$C的衰变规律的示意图(纵坐标$\frac{n}{{n}_{0}}$表示的是任意时刻放射性元素的原子数与t=0时的原子数之比),则该放射性元素的半衰期是5700年.若从某次考古时发掘出来的木材中,检测到所含${\;}_{6}^{14}$C的比例是正在生长的植物中的80%,则该古物距今约1900年.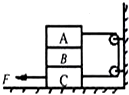 如图所示,轻绳两端分别与A、C两物体相连接,mA=1kg,mB=2kg,mC=3kg,物体A、B间的动摩擦因数均为μ1=0.5,B、C及C与地面间的动摩擦因数均为μ2=0.1,轻绳与滑轮间的摩擦可忽略不计.若要用力将C物匀速拉出,A与B始终相对静止,则作用在C物上水平向左的拉力大小为( )
如图所示,轻绳两端分别与A、C两物体相连接,mA=1kg,mB=2kg,mC=3kg,物体A、B间的动摩擦因数均为μ1=0.5,B、C及C与地面间的动摩擦因数均为μ2=0.1,轻绳与滑轮间的摩擦可忽略不计.若要用力将C物匀速拉出,A与B始终相对静止,则作用在C物上水平向左的拉力大小为( )