用如图所示的装置可以测量磁感应强度B的值.取一长方体金属块置于匀强磁场中.磁场方向垂直于金属块前后两个侧面.左右两侧面接入电路中.测得流过长方体金属块的电流大小为I.用理想电压表测得长方体上下两表面的电势差大小为U.已知长方体金属块的长.宽.高分别为a.b.c.查得该金属材料单位体积内的自由电子数为n.电子的电荷量为e.则可以测出磁感应强度B的值为$\frac{ 题目和参考答案——青夏教育精英家教网—

题目内容

4．

用如图所示的装置可以测量磁感应强度B的值，取一长方体金属块置于匀强磁场中，磁场方向垂直于金属块前后两个侧面，左右两侧面接入电路中，测得流过长方体金属块的电流大小为I，用理想电压表测得长方体上下两表面的电势差大小为U，已知长方体金属块的长、宽、高分别为a、b、c，查得该金属材料单位体积内的自由电子数为n，电子的电荷量为e，则可以测出磁感应强度B的值为$\frac{enbU}{I}$．

分析由电流的微观表达式求出电子的平均速率，应用平衡条件求出磁感应强度大小，从而即可求解．

解答解：由电流定义式：I=$\frac{△q}{△t}$=$\frac{enbcv•△t}{△t}$=enbcv，
则电子平均速率：v=$\frac{I}{enbc}$；
电子通过金属板，电子受到的电场力与洛伦兹力大小相等，方向相反，
则：evB=e$\frac{U}{c}$，
磁感应强度：B=$\frac{enbU}{I}$，
故答案为：$\frac{enbU}{I}$．

点评本题考查了求电子的速率、磁感应强度，应用电流的微观表达式、平衡条件、左手定则即可正确解题．

练习册系列答案

相关题目

10．

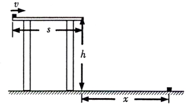如图所示，一书桌的水平桌面长s=0.5m，桌面离水平地面的高度h=0.8m，一个可视为质点的小物块从桌面左端以v=4m/s的水平初速度沿桌面向右滑行，小物块离开桌面后掉在地上，落地点到桌面右端边缘的水平距离x=1.2m，空气阻力忽略不计，g取10m/s²，求：
（1）小物块离开桌面右端边缘时的速度大小；
（2）小物块与桌面的动摩擦因数．

11．

如图所示，MPQO为有界的竖直向下的匀强电场（边界上有电场），电场强度为E=$\frac{mg}{q}$，ACB为光滑固定的半圆形绝緣轨道，轨道半径为R，O点是圆心，直径AB水平，A、B为直径的两个端点，AC为$\frac{1}{4}$圆弧．一个质童为m．电荷量为-q的带负电小球，从A点正上方高为R处由静止释放，从A点沿切线进入半圆轨道，不计空气阻力．求：
（1）小球到达C点时对轨道的压力；
（2）若E′=$\frac{2mg}{q}$，小球从A点正上方离A点至少多高处静止释放，才能使小球沿轨道运动到C点．

12．

如图，△OAC的三个顶点的坐标分别为0（0，0），A（L，0），C（0，$\sqrt{3}$L），在△OAC区域内有垂直于xOy平面向里的匀强磁场．在t=0时刻，同时从三角形的OA边各处以沿y轴正向的相同速度将质量均为m，电荷量均为q的带正电粒子射入磁场，已知在t=t₀时刻从OC边射出磁场的粒子的速度方向垂直于y轴．不计粒子重力和空气阻力及粒子间相互作用．
（1）求磁场的磁感应强度B的大小；
（2）若从OA边两个不同位置射入磁场的粒子，先后从OC边上的同一点P（P点图中未标出）射出磁场，求这两个粒子在磁场中运动的时间t₁与t₂之间应满足的关系．

19．

如图所示，在光滑水平面上固定一条形磁铁，有一个金属小球向磁铁方向运动，关于小球的速度变化，以下说法正确的是（　　）

	A．	如果小球是铁材料做的，则小球做减速运动
	B．	如果小球是铁材料做的，则小球做加速运动
	C．	如果小球是铜材料做的，则小球做减速运动
	D．	如果小球是铜材料做的，则小球做匀速运动

9．

某同学利用计算机绘制了a、b两个单摆在同一个实验室里的振动图象如图所示，可知两单摆摆长之比$\frac{{L}_{a}}{{L}_{b}}$=4：9．