题目内容
【题目】如图所示,光滑水平直轨道上两滑块A、B用橡皮筋连接,A的质量为m,开始时橡皮筋松弛,B静止,给A向左的初速度v0 , 一段时间后,B与A同向运动发生碰撞并黏在一起,碰撞后的共同速度是碰撞前瞬间A的速度的两倍,也是碰撞前瞬间B的速度的一半,求: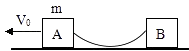
(i)B的质量;
(ii)碰撞过程中A、B系统机械能的损失.
【答案】解:(i)以初速度v0的方向为正方向,设B的质量为mB,A、B碰后的共同速度为v,
由题意知,碰撞前瞬间A的速度为 ![]() ,碰撞前瞬间B的速度为2v,由动量守恒定律得,
,碰撞前瞬间B的速度为2v,由动量守恒定律得,
![]() ①
①
由①式得, ![]() .②
.②
(ii)从开始到碰后的全过程,以初速度v0的方向为正方向,由动量守恒得,
mv0=(m+mB)v ③
设碰撞过程A、B系统机械能损失为△E,
则 ![]() ﹣
﹣ ![]() ,④
,④
联立②③④式得,△E= ![]()
答:(i)B的质量为 ![]() ;
;
(ii)碰撞过程中A、B系统机械能的损失为 ![]() .
.
【解析】对A、B碰撞前后过程运用动量守恒定律,抓住A、B碰撞前的瞬时速度和碰后的速度关系求出B的质量.
对整个过程运用动量守恒,求出最终的速度与A初速度的关系,再结合能量守恒求出碰撞过程中A、B系统机械能的损失.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目