��Ŀ����
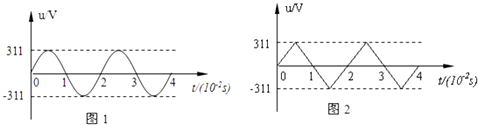
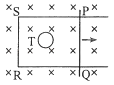
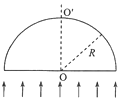
����Ŀ����ͼ����ʾ�������㹻�������費�ƵĹ⻬ƽ�н����������ΪL1=1m������ƽ����ˮƽ��ɦ�=30��ǣ��϶�������ֵR=1.5���ĵ��裻����Ϊm=0.2kg����ֵr=0.5�������ʽ�����ab�����������ϣ����뵼�����϶�ΪL2=4m�����뵼�촹ֱ���������ýӴ�������װ�ô���һ��ǿ�ų��У�����ǿ�ų������뵼��ƽ�洹ֱ���Ÿ�Ӧǿ�ȴ�С��ʱ��仯�������ͼ����ʾ����g=10m/s2��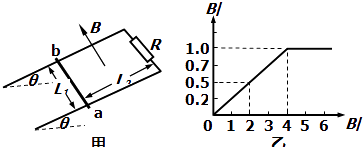
��1������ab����ֹ����0��4s�ڣ�ͨ��������ab�ĵ����������Σ�
��2��Ϊ�˱���ab����ֹ����Ҫ�ڰ����е�ʩ����һƽ���ڵ���ƽ�������F����t=2sʱ������F�Ĵ�С�ͷ���
��3��5s��ȥ����F�����������ɾ�ֹ��ʼ�»�����ʱ�õ�ѹ��������R���˵ĵ�ѹ��ʱ�ɼ�����������������ʾ����ʾ�ĵ�ѹ�ﵽijһ�㶨ֵ���¸�ʱ�̰���λ�ã������λ�������ʼλ�����2.4m�����������ʱ���ٶȼ��»�����λ�õĹ������ڵ���R�ϲ����Ľ����ȣ�
���𰸡�
��1��
�⣺��0��4s�ڣ��ɷ����ڵ�Ÿ�Ӧ���ɣ�
![]()
�ɱպϵ�·ŷķ���ɣ�
![]()
������a��b
��2��
�⣺��t=2sʱ��ab���ܵ���б�����ϵİ�����F��=BIL1=0.5��0.5��1N=0.25N
��ab��������������ƽ��������F+F����mgsin30��=0
F=mgsin30�㩁F��=��0.2��10��0.5��0.25��N=0.75N
�����ص���б������
��3��
�⣺ab���ص����»��и�Ÿ��߲�����Ӧ�綯�ƣ��У�E��=B��L1v
�����ĸ�Ӧ���� ![]()
���»����ٶ��ȶ�ʱ�������ε�ѹҲ�㶨����ʱab������ƽ�⣬
��mgsin30��=B��I��L1
��ã� ![]()
�ɶ��ܶ������� ![]()
![]()
�� ![]()
����������1����0��4s�ڣ��ɷ����ڵ�Ÿ�Ӧ���ɺͱպϵ�·ŷķ������⣮��2�����ݷ����ڵ�Ÿ�Ӧ�������0��4s�ڸ�Ӧ�綯�ƣ��ٸ��ݱպϵ�·ŷķ��������������Ӷ���������������ð��ӵ�ƽ���������F�Ĵ�С�ͷ���3��������ɾ�ֹ�»�����������֧�����������������»��ļ��ٶȼ�СΪ0ʱ���ٶ��ȶ�����ѹҲ�ȶ�������ƽ�������ʱ���ٶȣ��ٸ��������غ���������������ݵ���ʱ����ͬ�� ![]() ��
��