题目内容
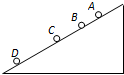
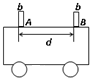
如图所示,为测量作匀加速直线运动小车的加速度,将宽度很小且均为b的挡光片A、B固定在小车上,测得二者间距为d(d远大于b);当小车匀加速经过固定在车旁的光电门时,测得两挡光片先后经过的时间分别为△t1和△t2,则小车的加速度a=______.

挡光片通过光电门的平均速度可以认为是小车在此时刻的瞬时速度,故小车两次同过光电门的速度分别为:
v1=
| b |
| △t1 |
| b |
| △t2 |
此段时间小车的位移为d,由运动学速度位移关系式得:
v22-v12=2ad
带入数据得:
(
| b |
| △t2 |
| b |
| △t1 |
解得:
a=
| b2 |
| 2d |
| 1 |
| △t22 |
| 1 |
| △t12 |
故答案为:
| b2 |
| 2d |
| 1 |
| △t22 |
| 1 |
| △t12 |

练习册系列答案
相关题目