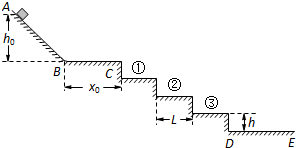题目内容
高台滑雪运动员经过一段弧长为s=
m的圆弧后,从圆弧上的O点水平飞出,圆弧半径R=10m,他在圆弧上的O点受到的支持力为820N.运动员连同滑雪板的总质量为50kg,他落到了斜坡上的A点,斜坡与水平面的夹角θ=37°,如右图所示.忽略空气阻力的影响,取重力加速度g=10m/s2,求:
(1)运动员离开O点时的速度大小?
(2)运动员在圆弧轨道上克服摩擦力做的功?
(3)运动员落到斜坡上的速度大小?

| 10π |
| 3 |
(1)运动员离开O点时的速度大小?
(2)运动员在圆弧轨道上克服摩擦力做的功?
(3)运动员落到斜坡上的速度大小?

(1)根据运动员在o点的受到重力和支撑力,
由牛顿第二定律得:FN-mg=
解得:v0=8m/s
(2)设圆弧对的圆心角为α,S=Rα,
解得:α=
运动员在圆弧上下滑的高度:h=R(1-cosα)=5m
设运动员在圆轨道上克服摩擦力做的功为Wf,
对运动员在圆弧上下滑的过程应用动能定理,
得:-Wf+mgh=
-0
解得:Wf=900J
(3)设A点与O点的距离为了l,运动员飞出后做平抛运动
水平方向:lcosθ=v0t
竖直方向:lsinθ=
gt2
解得:t=12s,vy=gt=12m/s
所以:V=
=
m/s
答:(1)运动员离开O点时的速度大小8m/s
(2)运动员在圆弧轨道上克服摩擦力做的功900J
(3)运动员落到斜坡上的速度大小
m/s
由牛顿第二定律得:FN-mg=
m
| ||
| R |
解得:v0=8m/s
(2)设圆弧对的圆心角为α,S=Rα,
解得:α=
| π |
| 3 |
运动员在圆弧上下滑的高度:h=R(1-cosα)=5m
设运动员在圆轨道上克服摩擦力做的功为Wf,
对运动员在圆弧上下滑的过程应用动能定理,
得:-Wf+mgh=
m
| ||
| 2 |
解得:Wf=900J
(3)设A点与O点的距离为了l,运动员飞出后做平抛运动
水平方向:lcosθ=v0t
竖直方向:lsinθ=
| 1 |
| 2 |
解得:t=12s,vy=gt=12m/s
所以:V=
|
| 208 |
答:(1)运动员离开O点时的速度大小8m/s
(2)运动员在圆弧轨道上克服摩擦力做的功900J
(3)运动员落到斜坡上的速度大小
| 208 |

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目