题目内容
 如图所示,直角玻璃三棱镜置于空气中,已知∠A=60°,∠C=90°;一束极细的光于 AC边的中点垂直AC面入射,
如图所示,直角玻璃三棱镜置于空气中,已知∠A=60°,∠C=90°;一束极细的光于 AC边的中点垂直AC面入射,. |
| AC |
| 2 |
(1)光在棱镜内经一次全反射后第一次射入空气时的折射角.
(2)光从进入棱镜到第一次射入空气时所经历的时间(设光在真空中传播速度为c).
分析:(1)画出光路图,由几何知识找出角度关系,由折射定律可以求解.
(2)运用几何关系求出光在棱镜中通过的路程s,由v=
求得光在棱镜中传播速度,由运动学知识求解时间.
(2)运用几何关系求出光在棱镜中通过的路程s,由v=
| c |
| n |
解答:解:(1)设临界角为C,则sinC=
=
,则得:C=45°.
如图所示,由几何知识得:∠2=60°>C=45°,所以光线在D点发生全反射.
由反射定律和几何知识得:∠4=30°,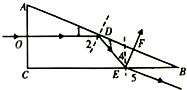
则 n=
则得:sin∠5=nsin∠4=
×sin30°=
所以第一次射入空气的折射角∠5=45°.
(2)设光线由O点到E点所需的时间t,则
光在棱镜的速度为:v=
=
c,
由数学知识得,光在棱镜中通过的路程为:s=OD+DE=
a+
a
则得:t=
=
.
答:
(1)光在棱镜内经一次全反射后第一次射入空气时的折射角.
(2)光从进入棱镜到第一次射入空气时所经历的时间为
.
| 1 |
| n |
| 1 | ||
|
如图所示,由几何知识得:∠2=60°>C=45°,所以光线在D点发生全反射.
由反射定律和几何知识得:∠4=30°,

则 n=
| sin∠5 |
| sin∠4 |
则得:sin∠5=nsin∠4=
| 2 |
| ||
| 2 |
所以第一次射入空气的折射角∠5=45°.
(2)设光线由O点到E点所需的时间t,则
光在棱镜的速度为:v=
| c |
| n |
| ||
| 2 |
由数学知识得,光在棱镜中通过的路程为:s=OD+DE=
| 3 |
2
| ||
| 3 |
则得:t=
| s |
| v |
5
| ||
| 3c |
答:
(1)光在棱镜内经一次全反射后第一次射入空气时的折射角.
(2)光从进入棱镜到第一次射入空气时所经历的时间为
5
| ||
| 3c |
点评:做光学类题目,一般要正确画出光路图,利用几何知识帮助我们分析角的大小,列式计算即可.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图所示,画有直角坐标系xOy的白纸位于水平桌面上,M是放在白纸上的半圆玻璃砖,其底面的圆心在坐标系原点,直边与x轴重合,OA是画在纸上的直线,P1、P2为竖直的插在直线OA上的两枚大头针,P3是竖直插在纸上的第三枚大头针,α是直线OA与y轴正方向的夹角,β是直线OP3与y轴负方向的夹角,只要直线OA画得合适,且P3的位置取得正确,测得角α、β便可求得玻璃的折射率.某学生在用上述方法测量玻璃的折射率时,在他画出的直线OA上竖直插上了P1、P2两枚大头针,但在y<0的区域内,不管眼睛放在何处,都无法透过玻璃看到P1、P2的像,他应采取的措施是
如图所示,画有直角坐标系xOy的白纸位于水平桌面上,M是放在白纸上的半圆玻璃砖,其底面的圆心在坐标系原点,直边与x轴重合,OA是画在纸上的直线,P1、P2为竖直的插在直线OA上的两枚大头针,P3是竖直插在纸上的第三枚大头针,α是直线OA与y轴正方向的夹角,β是直线OP3与y轴负方向的夹角,只要直线OA画得合适,且P3的位置取得正确,测得角α、β便可求得玻璃的折射率.某学生在用上述方法测量玻璃的折射率时,在他画出的直线OA上竖直插上了P1、P2两枚大头针,但在y<0的区域内,不管眼睛放在何处,都无法透过玻璃看到P1、P2的像,他应采取的措施是 (2013?商丘三模)如图所示,内径均匀的直角细玻璃管ABC两端开口,AB段竖直,BC段水平,AB=100cm,BC=40cm,在水平段BC内有一长10cm的水银柱,其左端距B点10cm,环境温度为330K时,保持BC段水平,将玻璃管A端缓慢竖直向下插入大水银槽中,使A端在水银面下10cm.已知大气压为75cmHg且保持不变,若环境温度缓慢升高,求温度升高到多少K时,水银柱刚好全部溢出.
(2013?商丘三模)如图所示,内径均匀的直角细玻璃管ABC两端开口,AB段竖直,BC段水平,AB=100cm,BC=40cm,在水平段BC内有一长10cm的水银柱,其左端距B点10cm,环境温度为330K时,保持BC段水平,将玻璃管A端缓慢竖直向下插入大水银槽中,使A端在水银面下10cm.已知大气压为75cmHg且保持不变,若环境温度缓慢升高,求温度升高到多少K时,水银柱刚好全部溢出.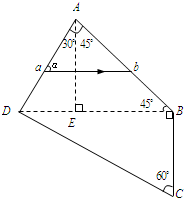 玻璃棱镜ABCD可以看成是由如图所示的ADE、ABE、BCD三个直角三棱镜组成,一束从AD面入射的光线在棱镜中的折射光线ab与AD面的夹角α=60°,已知光在真空的速度c=3×108m/s,玻璃的折射率n=1.5.求:
玻璃棱镜ABCD可以看成是由如图所示的ADE、ABE、BCD三个直角三棱镜组成,一束从AD面入射的光线在棱镜中的折射光线ab与AD面的夹角α=60°,已知光在真空的速度c=3×108m/s,玻璃的折射率n=1.5.求: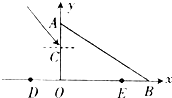 把某一直角玻璃棱镜AOB平放在坐标纸上,如图所示,用一细束红光掠过纸面从C点入射,经AO面反射和折射后,反射光线和折射光线与x轴交于D、E两点.已知C、D、E三点的坐标分别为(0,12)、(-9,0)、(16,0).由此可以计算出该棱镜材料对红光的折射率为( )
把某一直角玻璃棱镜AOB平放在坐标纸上,如图所示,用一细束红光掠过纸面从C点入射,经AO面反射和折射后,反射光线和折射光线与x轴交于D、E两点.已知C、D、E三点的坐标分别为(0,12)、(-9,0)、(16,0).由此可以计算出该棱镜材料对红光的折射率为( )