Question

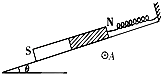
【题目】如图所示，一端固定在地面上的杆与水平方向夹角为θ.将一质量为M的滑块套在杆上，滑块通过轻绳悬挂一质量为m的小球，杆与滑块之间的动摩擦因数为μ，先给滑块一个沿杆方向的初速度.稳定后滑块和小球一起以共同的加速度沿杆运动，此时绳子与竖直方向的夹角为β，且β>θ，不计空气阻力.则滑块的运动情况是（ ）

A. 沿着杆减速下滑

B. 沿着杆减速上滑

C. 沿着杆加速下滑

D. 沿着杆加速上滑

Answer 1

【答案】B

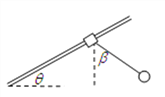
【解析】把环和球看做一个整体受力分析，沿斜面和垂直斜面建立直角坐标系得，

若速度方向向下，则

沿斜面方向：（m1+m2）gsinθ-f=（m1+m2）a 垂直斜面方向：FN=（m1+m2）gcosθ

摩擦力：f=μFN

联立可解得：a=gsinθ-μgcosθ，

对小球有：

a=gsinβ

所以gsinθ-μgcosθ=gsinβ

gsinθ-gsinβ=μgcosθ

因为θ＜β，所以gsinθ-gsinβ＜0，但μgcosθ＞0

所以假设不成立，即速度的方向一定向上

由于加速度方向向下，所以物体沿杆减速上滑，故B正确。

点晴：环与小球保持相对静止，并以相同的加速度a一起下滑，对整体进行受力分析求出加速度，采用隔离法，分析小球的受力，求出加速度，结合θ＜β分析即可判断。