题目内容
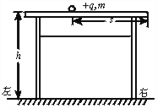
【题目】如图甲所示,轻杆OB可绕B点自由转动,另一端O点用细绳拉住,固定在左侧墙壁上,质量为m的重物用细绳OC悬挂在轻杆的O点,OA与轻杆的夹角∠BOA=30°.乙图中水平轻杆OB一端固定在竖直墙壁上,另一端O装有小滑轮,用一根绳跨过滑轮后悬挂一质量为m的重物,图中∠BOA=30°,求:
(1)甲、乙两图中细绳OA的拉力各是多大?
(2)甲图中轻杆受到的弹力是多大?
(3)乙图中轻杆对滑轮的作用力是多大?

【答案】(1)2mg;mg;(2)![]() ;(3)mg;
;(3)mg;
【解析】(1)图甲中,以O点为研究对象,受力分析,
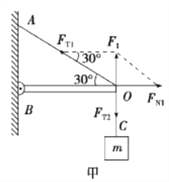
根据平衡条件得: ![]()
![]() ,,
,,
图乙中,对绳子上的O点分析:
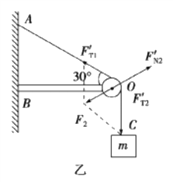
,受力平衡,有: ![]() ,
,
(2)由牛顿第三定律:图甲中OB杆受到的弹力![]()
(3)乙图中,根据题意可得,对O点受力分析: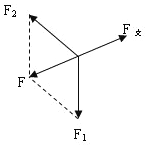
滑轮受到绳子的作用力应为图中两段绳中拉力F1和F2的合力F,
因同一根绳张力处处相等,都等于物体的重量,即![]() .
.
用平行四边形定则作图,因为拉力F1和F2的夹角为120°,则由几何知识得: ![]()
乙图中,由于平衡,则 轻杆对滑轮的作用力和轻绳对滑轮的作用力大小相等,方向相反,即![]()
综上所述本题答案是:(1)2mg;mg;(2)![]() ;(3)mg;
;(3)mg;

练习册系列答案
相关题目