题目内容
19. 如图所示,等腰三角形OPQ区域内存在场强方向沿PQ方向、大小为E的匀强电场,A为PQ的中点,D为OQ的中点,PQ=2L,θ=30°.一质量为m、电量为 q的带正电粒子(重力不计、初速度视为零),从无限靠近M板O′处由静止释放,经两平行金属板M、N间的电场加速后,通过N板上的小孔沿AO方向从A点射入三角形OPQ区域,粒子恰好从D点射出电场.
如图所示,等腰三角形OPQ区域内存在场强方向沿PQ方向、大小为E的匀强电场,A为PQ的中点,D为OQ的中点,PQ=2L,θ=30°.一质量为m、电量为 q的带正电粒子(重力不计、初速度视为零),从无限靠近M板O′处由静止释放,经两平行金属板M、N间的电场加速后,通过N板上的小孔沿AO方向从A点射入三角形OPQ区域,粒子恰好从D点射出电场.(1)求M、N两板间的电压U及粒子过A点时的速率υ;
(2)若将三角形OPQ区域内的电场撤去,在此区域内及其边界上充满方向垂直纸面向里的匀强磁场,该粒子仍从O′处由静止释放,要使该粒子在三角形OPQ区域中运动的时间最长,磁场的磁感应强度B应为多大?并求在磁场中运动的最长时间tm.
分析 (1)因做类平抛运动,则由两个方向上分别列位移方程求解.
(2)由运动轨迹确定运动圆的半径,再由洛伦兹力提供向心力确定B,由周期公式得时间.
解答 解:(1)粒子在两板间电场加速,根据动能定理有:
qU=$\frac{1}{2}$mυ2
粒子在三角形OPQ区域中做类平抛运动,有:
$\frac{L}{2}$=$\frac{1}{2}$at2
$\frac{1}{2}$Ltanθ=υt
根据牛顿第二定律有:qE=ma
解得:U=$\frac{1}{24}$EL,
υ=$\sqrt{\frac{qEL}{12m}}$. (2)由t=$\frac{s}{υ}$知,当υ一定时,弧长s最大即轨迹圆弧恰好与OP边相切(如图所示)时t最大.设轨迹圆弧与OP边相切时圆弧的半径为R,有:
(2)由t=$\frac{s}{υ}$知,当υ一定时,弧长s最大即轨迹圆弧恰好与OP边相切(如图所示)时t最大.设轨迹圆弧与OP边相切时圆弧的半径为R,有:
R+$\frac{R}{sinθ}$=L
qυB=m$\frac{υ2}{R}$
tm=$\frac{πR}{υ}$
解得:B=$\sqrt{\frac{3mE}{4qL}}$
tm=$2π\sqrt{\frac{mL}{3qE}}$
答:(1)M、N两板间的电压U为$\frac{1}{24}$EL,及粒子过A点时的速率为$\sqrt{\frac{qEL}{12m}}$.
(2)磁场的磁感应强度B为$\sqrt{\frac{3mE}{4qL}}$ 磁场中运动的最长时间为$2π\sqrt{\frac{mL}{3qE}}$.
点评 处理带电粒子在磁场中运动问题,关键作出粒子的运动轨迹,会确定圆周运动的圆心、半径、圆心角,结合半径公式、周期公式进行求解.

练习册系列答案
相关题目
14. 如图所示,质量分别为m1和m2两个物体用两根轻质细线,分别悬挂在天花板上的A、B两点,两线与水平方向夹角分别为α,β且α>β,两物体间的轻质弹簧恰好处于水平状态,两根绳子拉力分别为TA和TB,则下列说法正确的是( )
如图所示,质量分别为m1和m2两个物体用两根轻质细线,分别悬挂在天花板上的A、B两点,两线与水平方向夹角分别为α,β且α>β,两物体间的轻质弹簧恰好处于水平状态,两根绳子拉力分别为TA和TB,则下列说法正确的是( )
 如图所示,质量分别为m1和m2两个物体用两根轻质细线,分别悬挂在天花板上的A、B两点,两线与水平方向夹角分别为α,β且α>β,两物体间的轻质弹簧恰好处于水平状态,两根绳子拉力分别为TA和TB,则下列说法正确的是( )
如图所示,质量分别为m1和m2两个物体用两根轻质细线,分别悬挂在天花板上的A、B两点,两线与水平方向夹角分别为α,β且α>β,两物体间的轻质弹簧恰好处于水平状态,两根绳子拉力分别为TA和TB,则下列说法正确的是( )| A. | TA=TB | B. | TA<TB | C. | m1=m2 | D. | m1>m2 |
4.某小型水电站的电能输送示意图如下.发电机的输出电压为220V,输电线总电阻为r,升压变压器原副线圈匝数分别为n1、n2.降压变压器原副线匝数分别为n3、n4(变压器均为理想变压器).要使额定电压为220V的用电器正常工作,则( )


| A. | $\frac{{n}_{2}}{{n}_{1}}$<$\frac{{n}_{3}}{{n}_{4}}$ | |
| B. | $\frac{{n}_{2}}{{n}_{1}}$>$\frac{{n}_{3}}{{n}_{4}}$ | |
| C. | 升压变压器的输出电压等于降压变压器的输入电压 | |
| D. | 升压变压器的输出功率大于降压变压器的输入功率 |
11.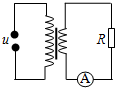 如图所示,理想变压器原、副线圈的匝数比是10:1,原线圈输入交变电压u=100$\sqrt{2}$sin50πt(V),在副线圈中接有理想电流表和定值电阻R,电阻阻值R=10Ω,关于电路分析,下列说法中正确的是( )
如图所示,理想变压器原、副线圈的匝数比是10:1,原线圈输入交变电压u=100$\sqrt{2}$sin50πt(V),在副线圈中接有理想电流表和定值电阻R,电阻阻值R=10Ω,关于电路分析,下列说法中正确的是( )
 如图所示,理想变压器原、副线圈的匝数比是10:1,原线圈输入交变电压u=100$\sqrt{2}$sin50πt(V),在副线圈中接有理想电流表和定值电阻R,电阻阻值R=10Ω,关于电路分析,下列说法中正确的是( )
如图所示,理想变压器原、副线圈的匝数比是10:1,原线圈输入交变电压u=100$\sqrt{2}$sin50πt(V),在副线圈中接有理想电流表和定值电阻R,电阻阻值R=10Ω,关于电路分析,下列说法中正确的是( )| A. | 交流电的频率为50Hz | |
| B. | 电流表示数是$\sqrt{2}$A | |
| C. | 电阻R消耗的电功率为10W | |
| D. | 若用电容器替代电阻R,则该电容器的耐压值至少是10V |
7. 将两个质量均为m的小球a,b用细线相连后,两用细线悬挂于O点,如图所示,用力F拉小球b,使两个小球都处于静止状态,且保持细线Oa与竖直方向的夹角为37°,则力F在各种可能的方向中,最小值为( )
将两个质量均为m的小球a,b用细线相连后,两用细线悬挂于O点,如图所示,用力F拉小球b,使两个小球都处于静止状态,且保持细线Oa与竖直方向的夹角为37°,则力F在各种可能的方向中,最小值为( )
 将两个质量均为m的小球a,b用细线相连后,两用细线悬挂于O点,如图所示,用力F拉小球b,使两个小球都处于静止状态,且保持细线Oa与竖直方向的夹角为37°,则力F在各种可能的方向中,最小值为( )
将两个质量均为m的小球a,b用细线相连后,两用细线悬挂于O点,如图所示,用力F拉小球b,使两个小球都处于静止状态,且保持细线Oa与竖直方向的夹角为37°,则力F在各种可能的方向中,最小值为( )| A. | $\frac{8}{5}$mg | B. | $\frac{4}{5}$mg | C. | $\frac{6}{5}$mg | D. | $\frac{3}{5}$mg |
8.在做“单摆测重力加速度”的实验时,可能导致重力加速度的测量结果偏大的有( )
| A. | 振幅偏小 | |
| B. | 在未悬挂摆球之前先测定好摆长 | |
| C. | 摆球做圆锥摆运动 | |
| D. | 将摆线长和球的直径之和当成了摆长 |
