题目内容
双星系统由两颗恒星组成,两恒星在相互引力的作用下分别围绕其连线上的某一点做周期相同的匀速圆周运动。研究发现,双星系统演化过程中两星的总质量、距离和周期均可能发生变化。若某双星系统中两星做圆周运动的周期为T,经过一段时间演化后,两星总质量变为原的k倍,两星之间的距离变为原的n倍,则此时圆周运动的周期为 ( )
A. | B. | C. | D. |
B
解析试题分析:设m1的轨道半径为R1,m2的轨道半径为R2.由于它们之间的距离恒定,因此双星在空间的绕向一定相同,同时角速度和周期也都相同.由向心力公式可得:
对m1: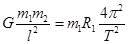 ①
①
对m2: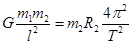 ②
②
又因为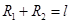 ,
,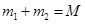 ,由①②式可得
,由①②式可得 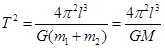
所以当两星总质量变为KM,两星之间的距离变为原来的n倍,圆周运动的周期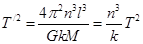 ,即
,即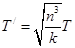 T,故ACD错误,B正确;
T,故ACD错误,B正确;
考点:万有引力定律及其应用。

 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案人造地球卫星绕地球做匀速圆周运动,线速度减小,仍然做匀速圆周运动,则
| A.离地面越近 | B.角速度越大 |
| C.周期越大 | D.向心加速度越大 |
我国的航天事业发展迅速,到目前为止,我们不仅有自己的同步通信卫星,也有自主研发的“神舟”系列飞船,还有自行研制的全球卫星定位与通信系统(北斗卫星导航系统)。其中“神舟”系列飞船绕地球做圆轨道飞行的高度仅有几百千米;北斗卫星导航系统的卫星绕地球做圆轨道飞行的高度达2万多千米。对于它们运行过程中的下列说法正确的是
| A.“神舟”系列飞船的加速度小于同步卫星的加速度 |
| B.“神舟”系列飞船的角速度小于同步通信卫星的角速度 |
| C.北斗导航系统的卫星运行周期一定大于“神舟”系列飞船的运行周期 |
| D.同步卫星所受的地球引力一定大于北斗导航系统的卫星所受的地球引力 |
1990年5月,紫金山天文台将他们发现的第2752号小行星命名为吴健雄星,该小行星的半径为16km.若将此小行星和地球均看成质量分布均匀的球体,小行星密度和地球相同,已知地球半径R=6400km,地球表面重力加速度为g.这个小行星表面的重力加速度为
A. | B.400g | C.20g; | D. |
设地球赤道上随地球自转的物体线速度为v1,周期为T1;地面附近卫星线速度为v2,周期为T2;地球同步卫星线速度为v3,周期为T3;月亮线速度为v4,周期为T4。则以下关系正确的是( )
A. | B. |
C.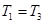 | D.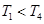 |
“嫦娥一号”月球卫星于2007年10月24日18时05分在中国西昌卫星发射中心用长征三号甲运载火箭发射成功。卫星将在地球轨道近地点上经历三次加速变轨后由地月转移轨道进入月球轨道。在月球轨道近月点上经历三次近月制动,进入127分钟工作轨道,如图所示。下列有关“嫦娥一号”月球卫星的论述正确的是
| A.卫星在地球轨道上变轨后机械能增大 |
| B.卫星在地球轨道上变轨后运行周期变小 |
| C.卫星在月球轨道上变轨后机械能增大 |
| D.卫星在月球轨道上变轨后运行周期变大 |
把火星和地球绕太阳运行的轨道视为圆周,由火星和地球绕太阳运动的周期之比可求得( )
| A.火星和地球的质量之比 |
| B.火星和太阳的质量之比 |
| C.火星和地球到太阳的距离之比 |
| D.火星和地球绕太阳运行速度大小之比 |
假设地球的质量不变,半径增大到原来的2倍,那么从地球发射人造卫星的第一宇宙速度的大小应为原来的
A.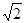 倍 倍 | B. 倍 倍 | C.1/2倍 | D.2倍 |
 的土星上空离土星表面高
的土星上空离土星表面高 的圆形轨道上绕土星飞行,环绕
的圆形轨道上绕土星飞行,环绕 周飞行时间为
周飞行时间为 。已知万有引力常量为
。已知万有引力常量为 ,则下列关于土星质量
,则下列关于土星质量 和平均密度
和平均密度 的表达式正确的是( )
的表达式正确的是( )


