题目内容
甲、乙 两颗人造地球卫星在同一轨道平面上的不同高度处同向运行,甲距地面高度为地球半径的0.5倍,乙甲距地面高度为地球半径的5倍,两卫星在某一时刻正好位于地球表面某处的正上空,试求:(1)两卫星运行的速度之比;
(2)乙卫星至少经过多少周期时,两卫星间的距离达到最大?
【答案】分析:卫星的向心力由万有引力提供,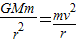 ,即可求出它们的速度关系;卫星间的距离第一次最大时,它们转过的角度差π.
,即可求出它们的速度关系;卫星间的距离第一次最大时,它们转过的角度差π.
解答:解:(1)卫星的向心力由万有引力提供,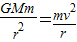 ,
,
得: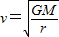
所以: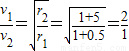
(2)卫星的向心力由万有引力提供: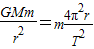
得: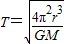
所以: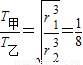
又因为卫星间的距离第一次最大时,它们转过的角度差π: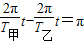
解得: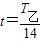
答:(1)两卫星运行的速度之比2:1;
(2)乙卫星至少经过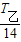 周期时,两卫星间的距离达到最大.
周期时,两卫星间的距离达到最大.
点评:该题考查万有引力定律的一般应用,其中卫星间的距离第一次最大时,它们转过的角度差π是解决问题的关键.属于中档题目.
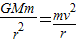 ,即可求出它们的速度关系;卫星间的距离第一次最大时,它们转过的角度差π.
,即可求出它们的速度关系;卫星间的距离第一次最大时,它们转过的角度差π.解答:解:(1)卫星的向心力由万有引力提供,
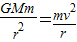 ,
,得:
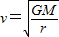
所以:
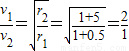
(2)卫星的向心力由万有引力提供:
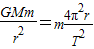
得:
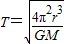
所以:
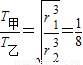
又因为卫星间的距离第一次最大时,它们转过的角度差π:
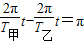
解得:
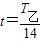
答:(1)两卫星运行的速度之比2:1;
(2)乙卫星至少经过
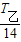 周期时,两卫星间的距离达到最大.
周期时,两卫星间的距离达到最大.点评:该题考查万有引力定律的一般应用,其中卫星间的距离第一次最大时,它们转过的角度差π是解决问题的关键.属于中档题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目