题目内容
【题目】如图示，圆管构成的半圆形竖直轨道和光滑斜面固定在水平地面上，圆形轨道半径和斜面高度均为R，斜面倾角a 等于45°，MN为直径且与水平面垂直。直径略小于圆管内径质量为m的小球以某一初速度冲进轨道，到达半圆轨道最高点M时飞出轨道，恰好落在光滑斜面顶端，并刚好沿光滑斜面下滑，重力加速度为g，忽略圆管内径及各处摩擦，求：
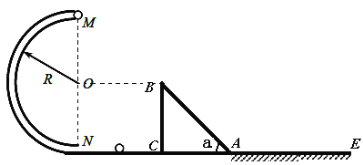
（1）小球在半圆轨道最高点M时所受弹力
（2）若AE段为摩擦因素等于ｕ的粗糙平面且足够长，且小球过A点速度大小不变,则小球在AE段滑行的距离是多少。
【答案】(1)mg(2)3R/u
【解析】(1)小球平抛运动到达斜面顶端时速度与水平方向成45度角，水平速度与竖直分速度相等，由竖直分运动
可求得水平速度，再由
可求得弹力为mg，方向向下
（2）小球落到B点时速度为
，由B到AE面静止，由动能定理有：mgR-
可得s=3R/u
练习册系列答案
相关题目
