题目内容
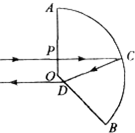
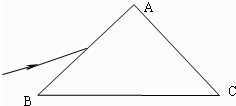
如图所示,三角形ABC为一棱镜的截面,∠A=60°、∠B=90°,棱镜折射率n=1.5.一细光束沿图中DE方向射到棱镜的AB界面上,入射点E为AB中点,AB长为L,入射角的正弦值sini=0.75,光速c=3x108m/s.求:
I.光在棱镜中传播的速率;
II.此束光射入棱镜后第一次射出棱镜的位置到C点的距离.

I.光在棱镜中传播的速率;
II.此束光射入棱镜后第一次射出棱镜的位置到C点的距离.

Ⅰ、由v=
得:
v=2×108m/
Ⅱ、入射光线在AB界面产生折射,由sini=nsinα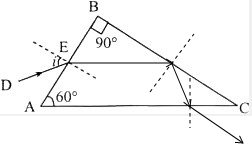
得:α=30°
结合几何关系得:β=60°
由sinC=
可知C<60°
所以光线在BC界面发生全反射,
而θ=30°<C,管线在AC界面第一次射出,结合几何关系可得射出点到C点的距离为
答:Ⅰ、光在棱镜中传播的速率为2×108m/s;
II.此束光射入棱镜后第一次射出棱镜的位置到C点的距离为
.
| c |
| n |
v=2×108m/
Ⅱ、入射光线在AB界面产生折射,由sini=nsinα

得:α=30°
结合几何关系得:β=60°
由sinC=
| 1 |
| n |
所以光线在BC界面发生全反射,
而θ=30°<C,管线在AC界面第一次射出,结合几何关系可得射出点到C点的距离为
| L |
| 2 |
答:Ⅰ、光在棱镜中传播的速率为2×108m/s;
II.此束光射入棱镜后第一次射出棱镜的位置到C点的距离为
| L |
| 2 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

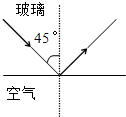
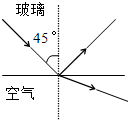
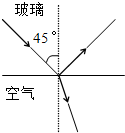
 ,一足够强的细光束在过球心的平面内以45°入射角由真空射入玻璃球。
,一足够强的细光束在过球心的平面内以45°入射角由真空射入玻璃球。