题目内容
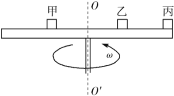
【题目】如图所示,一水平转台以恒定的角速度绕中心轴线![]() 匀速转动.现将甲、乙、丙三个物块放在台面上,三个物块均与转台保持相对静止.已知三物块与转台之间的动摩擦因数相等,质量关系为
匀速转动.现将甲、乙、丙三个物块放在台面上,三个物块均与转台保持相对静止.已知三物块与转台之间的动摩擦因数相等,质量关系为![]() ,到转轴的距离关系为
,到转轴的距离关系为![]() .则下列说法正确的是( )
.则下列说法正确的是( )
A.物块丙受到的静摩擦力小于物块甲受到的静摩擦力
B.物块乙受到的静摩擦力最小
C.物块丙的向心加速度最大
D.如果转台的转速逐渐变大,则最先发生相对滑动的为物块甲
【答案】BC
【解析】
假设物块乙、丙的质量分别为m,则物块甲的质量为![]() ,物块甲、乙的运动半径为r,则物块丙的运动半径为2r,由题意可知甲、乙、丙三个物块转动的角速度
,物块甲、乙的运动半径为r,则物块丙的运动半径为2r,由题意可知甲、乙、丙三个物块转动的角速度![]() 相等,发生相对滑动前,均由静摩擦力提供其做圆周运动的向心力,根据
相等,发生相对滑动前,均由静摩擦力提供其做圆周运动的向心力,根据![]() 知,物块甲所受的静摩擦力
知,物块甲所受的静摩擦力
![]()
物块乙所受的静摩擦力
![]()
物块丙所受的静摩擦力
![]()
显然物块甲与物块丙所受的静摩擦力大小相等,物块乙所受的静摩擦力最小,故A错误,B正确;
C.向心加速度![]() ,又由题意知物块丙的运动半径最大,则物块丙的向心加速度最大,故C正确;
,又由题意知物块丙的运动半径最大,则物块丙的向心加速度最大,故C正确;
D.根据
![]()
得,物块的转速
![]()
物块丙的运动半径最大,发生相对滑动的临界转速最小,可知转台的转速逐渐变大时,物块丙最先开始滑动,故D错误。
故选BC。

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目