Question

【题目】如图所示，一斜面体固定在水平地面上，倾角为θ=30°，高度为h=1.5m.一簿木板B置于斜面顶端，恰好能保持静止，木板下端连接有一根自然长度为L0=0.2m的轻弹弹簧，木板总质量为m=1kg，总长度为L=2.0m.一质量为M=3kg的小物块A从斜面体左侧某位置水平抛出，该位置离地高度H=1.7m，物块A经过一段时间后从斜面项端沿平行于斜面方向落到木板上并开始向下滑行，已知A、B之间的动摩擦因数，木板下滑到斜面底端碰到挡板时立刻停下，物块A最后恰好能脱离弹簧，且弹簧被压缩时一直处于弹性限度内，最大静摩擦力可认为等于滑动擦力，取重力加速度g=10，不计空气阻力。求：

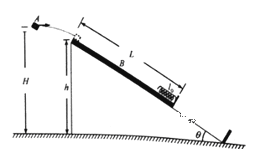
(1)物块A落到木板上的速度大小v；

(2)木板与挡板碰撞前的瞬间,木板和物块的速度大小；

(3)弹簧被压结到最短时的弹性势能。

Answer 1

【答案】（1） （2）VA=VB=3m/s （3）5J

【解析】

（1）物块A落到木板前做平抛运动，竖直方向：2g(Hh)＝vy2，
得：vy＝2m/s
物块A落到木板时的速度大小为：v＝＝4m/s
（2）由木板恰好静止在斜面上，得到斜面与木板间的摩擦因数μ0应满足：
mgsin30°＝μ0mgcos30°
得：μ0＝tan30°＝
物块A在木板上滑行时，以A为对象有： （沿斜面向上）
以木板B为对象有： （沿斜面向下）
假设A与木板达到v共时，A还没有压缩弹簧且木板还没有到达底端，则有：

解得：v共＝3m/s，t=0.4s
（3）此过程，，

故 ，说明以上假设成立
共速后，由于（M+m）gsin30°=μ0（M+m）gcos30°，A与木板B一起匀速到木板与底端挡板碰撞，木板停下，此后A做匀减速到与弹簧接触的过程，设接触弹簧时A的速度为vA，有：
解得：vA＝2m/s
设弹簧最大压缩量为xm，A从开始压缩弹簧到刚好回到原长过程有：
Q＝2μMgxmcos30°=MvA2
得：Q=6J，

A从开始压缩弹簧到弹簧最短过程有：

即弹簧压缩到最短时的弹性势能为5J