题目内容
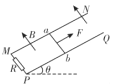
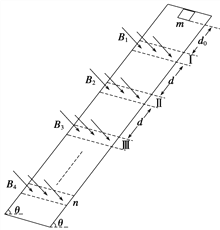
【题目】如图所示,足够长的斜面与水平面的夹角为θ=53°,空间中自上而下依次分布着垂直斜面向下的匀强磁场区域Ⅰ、Ⅱ、Ⅲ、……、n,相邻两个磁场的间距均为d=0.5 m.一边长L=0.1 m、质量m=0.5 kg、电阻R=0.2 Ω的正方形导线框放在斜面的顶端,导线框的下边距离磁场Ⅰ的上边界为d0=0.4 m,导线框与斜面间的动摩擦因数μ=0.5.将导线框由静止释放,导线框在每个磁场区域中均做匀速直线运动.已知重力加速度g=10 m/s2,sin 53°=0.8,cos 53°=0.6,求:
(1)导线框进入磁场Ⅰ时的速度;
(2)磁场Ⅰ的磁感应强度B1;
(3)磁场区域n的磁感应强度Bn与B1的函数关系.
【答案】(1)2m/s;(2)5T(3)![]()
【解析】试题分析:对线框研究,运用动能定理求出导线框进入磁场 I 时的速度;线框进入磁场后受重力、支持力、安培力和摩擦力,根据共点力平衡,结合闭合电路欧姆定律、切割产生的感应电动势公式求出磁感应强度的大小;线框在相邻两个磁场之间加速的距离相等,根据动能定理求出线框进入第n个磁场时的速度,结合共点力平衡,知在每个磁场中所受的安培力均相等,从而求出磁感应强度的表达式。
(1)线框从静止开始运动至刚进入磁场Ⅰ时,以线框为研究对象
由动能定理:![]()
解得: v1=2 m/s
(2)线框在磁场Ⅰ中做匀速直线运动,由法拉第电磁感应定律:
由法拉第电磁感应定律:E1=B1Lv1
由闭合电路欧姆定律:![]()
线框受到安培力:F1=B1I1L
由平衡条件有:mgsin θ-μmgcos θ-F1=0
解得:B1=5 T
(3)线框在相邻两个磁场之间加速的距离均为(d-L)=d0,线框由静止开始运动至刚进入第n个磁场时,由动能定理:![]()
又由上可得线框在第一个磁场Ⅰ中受到的安培力![]()
线框在第n个磁场受到的安培力:![]()
线框在每个磁场区域中均做匀速直线运动,受到的安培力均相等:Fn=F1
得:![]()

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案