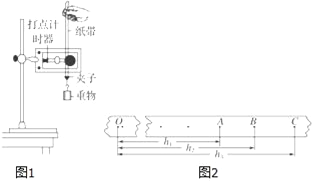
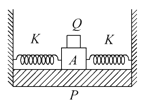
题目内容
【题目】如图所示，轻直杆OC的中点悬挂一个弹簧振子，其固有频率为2 Hz，杆的O端有固定光滑轴，C端下边由凸轮支持，凸轮绕其轴转动，转速为n。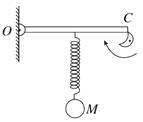
①在n从0逐渐增大到5 r/s的过程中，振子M的振幅变化情况将是怎样的？。
②当n＝r/s时振幅最大。
③若转速稳定在5 r/s，M的振动周期是。
【答案】其振幅先变大再变小；2；0.2 s
【解析】(1)当凸轮转速为 
时，它给弹簧振子的驱动力的频率为 
，当驱动力频率逐渐接近弹簧振子的固有频率时，其振幅逐渐增大，当 
逐渐远离 
时，其振幅逐渐减小。因此，在n从0逐渐增大到 
的过程中，其振幅先变大再变小。(2)当 
时，振幅最大，即 
时。(3)当 时，此时振子做受迫振动，其振动频率 
，其振动周期为 
。
【考点精析】掌握受迫振动和共振是解答本题的根本，需要知道迫振动的特点:受迫振动稳定时，系统振动的频率等于驱动力的频率，跟系统的固有频率无关；共振的条件:驱动力的频率等于振动系统的固有频率．
练习册系列答案
相关题目
【题目】一个小球沿斜面向下运动，现在用 
的闪频相机拍摄下的不同时刻的小球所处的位置照片如图所示，测得小球的在连续相等的时间内的位移如表，则：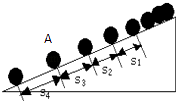
s1 | s2 | s3 | s4 |
8.20cm | 9.30cm | 10.40cm | 11.50cm |
（1）小球在相邻的相等时间内的位移差（填写“相等”或“不相等”），小球的运动性质属于直线运动．
（2）有甲、乙两个同学计算小球的加速度的方法如下：
甲： 
， 
， 
， 
；
乙： 
， 
， 
；
撇开本题所给的数据从理论上讲，甲、乙两位同学的计算方法中（填写“甲、乙”）方法更好，本题中小球的加速度值为 m/s2 ， 求经过A点处速度为m/s．
