题目内容
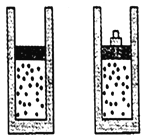
【题目】木块A、B分别重50N和60N,它们与水平地面之间的动摩擦因数均为0.25;夹在A、B之间的轻弹簧被压缩了2cm,弹簧的劲度系数为400N/m.系统置于水平地面上静止不动.现用F=1N的水平拉力作用在木块B上,如图所示,求力F作用后木块A、B所受摩擦力的大小.![]()
【答案】解:未加F时,木块AB受力平衡,所受静摩擦力等于弹簧的弹力,则弹簧弹力为:F1=kx=400N/m×0.02m=8N;
B木块与地面间的最大静摩擦力为:fBm=μGB=0.25×60N=15N;
而A木块与地面间的最大静摩擦力为:fAm=μGA=0.25×50N=12.5N;
施加F后,对木块B有:F+F1<fBm;
木块B受摩擦力仍为静摩擦力,其大小为fB=1N+8N=9N,
施加F后,木块A所受摩擦力仍为静摩擦力,大小为fA=8N;
答:力F作用后木块A所受摩擦力的大小8N,B所受摩擦力的大小9N.
【解析】先求解出木块A、B的最大静摩擦力,然后求解出弹簧弹力,最后对两个木块分别受力分析后分析求解.
【考点精析】关于本题考查的滑动摩擦力,需要了解滑动摩擦力:利用公式f=μF N 进行计算,其中FN 是物体的正压力,不一定等于物体的重力,甚至可能和重力无关.或者根据物体的运动状态,利用平衡条件或牛顿定律来求解才能得出正确答案.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目