题目内容
1.如图甲所示,弯曲部分AB和CD是两个半径都为0.3m的$\frac{1}{4}$圆弧轨道,中间的BC段是竖直的薄壁细圆管(细圆管内径略大于小球的直径)轨道,分别与上下圆弧轨道相切连接,BC段的长度L为0.2m.下圆弧轨道与水平轨道相切,其中D、A分别是上下圆弧轨道的最高点与最低点,整个轨道固定在竖直平面内.有一质量为0.3kg的小球以一定的速度沿水平轨道向右运动并从A点进入圆弧,不计小球运动中的一切阻力,求:(1)如果小球从D点以5m/s的速度水平飞出,求落地点与D点的水平距离;
(2)如果小球从D点以5m/s的速度水平飞出,求小球过圆弧A点时对轨道的压力;
(3)如果在D点右侧平滑连接一半径R=0.4m的半圆形光滑轨道DEF,如图乙所示,要使小球不脱离轨道运动,求小球在水平轨道上向右运动的速度大小范围(计算结果可以用根式表示).
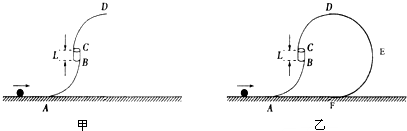
分析 (1)小球从D点以5m/s的速度水平飞出后做平抛运动,由平抛运动的规律可求得落地点与D点的水平距离;
(2)根据机械能守恒定律可求得小球经过A点的速度,在A点,由合力提供向心力,由牛顿定律求小球过圆弧A点时对轨道的压力;
(3)要使小球不脱离轨道,则小球可能由C点返回A点,也可能超过D点后沿DEF轨道回到A点,根据临界条件和机械能守恒定律可求得初速度的范围.
解答 解:(1)小球从D点以5m/s的速度水平飞出后做平抛运动,由平抛运动规律可得:
h=$\frac{1}{2}g{t}^{2}$
据题 h=2R+L=2×0.3m+0.2m=0.8m
代入数据解得 t=0.4s
所以落地点与D点的水平距离 x=vDt=5×0.4m=2m;
(2)由A到D的过程,由机械能守恒定律可得:
mgh+$\frac{1}{2}$mvD2=$\frac{1}{2}$mvA2
在A点,由牛顿第二定律可得:
N-mg=m$\frac{{v}_{A}^{2}}{R}$;
联立解得 N=44N
由牛顿第三定律知,小球过圆弧A点时对轨道的压力 N′=N=44N
(3)计论一:
小球进入轨道最高运动到C点,之后原路返回,由机械能守恒定律,有:
mg(R+L)=$\frac{1}{2}$mv12
得 v1=$\sqrt{10}$m/s
讨论二:小球进入轨道后恰好能通过圆弧最高点D,之后沿DEF运动而不脱离轨道,在D点,有
mg=m$\frac{{v}^{2}}{R}$
其中R=0.4m
从A到D由机械能守恒定律可得:
有:mgh+$\frac{1}{2}$mv2=$\frac{1}{2}$mv22
得 v2=2$\sqrt{5}$m/s
所以要使小球在运动过程中能不脱离轨道,初速度大小的范围为:v1≤$\sqrt{10}$m/s或v2≥2$\sqrt{5}$m/s
答:
(1)如果小球从D点以5m/s的速度水平飞出,落地点与D点的水平距离为2m
(2)如果小球能从D点以5m/s的速度水平飞出,小球过圆弧A点时对轨道的压力是44N.
(3)要使小球在运动过程中能不脱离轨道,初速度大小的范围是v1≤$\sqrt{10}$m/s或v2≥2$\sqrt{5}$m/s.
点评 本题考查机械能守恒定律的应用以及平抛运动规律的应用,要注意正确分析物理过程,正确进行受力分析,再通过平衡条件等选择正确的物理规律列式求解.关键要注意正确选择物理过程和规律.

| A. | 0.9A,0.15A | B. | 0.15A,0.9A | C. | 0.1A,0.6A | D. | 0.6A,0.1A |
| A. | 在5Ω到10Ω之间 | B. | 在2Ω到10Ω之间 | C. | 小于2Ω | D. | 大于20Ω |
| A. | 不断上坡和下坡的曲线运动 | B. | 匀速直线运动 | ||
| C. | 沿某一方向的直线运动 | D. | 在一直线上的往复运动 |
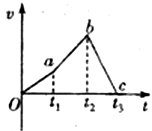
| A. | 0-t1时间内火箭的速度变化比t1:t2时间内慢 | |
| B. | 在0-t2时间内火箭上升,t2:t3时间内火箭下落 | |
| C. | t2时刻火箭离地面最高 | |
| D. | t3时刻火箭离地面最高 |
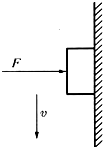 在水平力F作用下,重为G的物体匀速沿墙壁下滑,如图所示:若物体与墙壁之间的动摩擦因数为μ,则物体所受的摩擦力的大小为( )
在水平力F作用下,重为G的物体匀速沿墙壁下滑,如图所示:若物体与墙壁之间的动摩擦因数为μ,则物体所受的摩擦力的大小为( )| A. | μF | B. | μF+G | C. | G | D. | $\sqrt{{F^2}+{G^2}}$ |
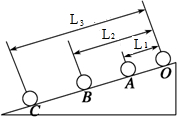 一小球从固定斜面的顶端以恒定的加速度滚下,某同学用频闪频率为10Hz的数码相机拍摄到的照片(是实际尺寸的十分之一)如图所示,其中照片中L1=0.5cm,L2=1.2cm,L3=2.1cm,根据照片给予的信息,请回答下列问题:
一小球从固定斜面的顶端以恒定的加速度滚下,某同学用频闪频率为10Hz的数码相机拍摄到的照片(是实际尺寸的十分之一)如图所示,其中照片中L1=0.5cm,L2=1.2cm,L3=2.1cm,根据照片给予的信息,请回答下列问题: